题目内容
7.关于x的方程$\frac{mx}{x-3}$=$\frac{3}{x-3}$无解,则m的值是1或0.分析 先把分式方程化为整式方程得到mx=3,由于关于x的分式方程$\frac{mx}{x-3}$=$\frac{3}{x-3}$无解,当x=3时,最简公分母x-3=0,将x=3代入方程mx=3,解得m=1,当m=0时,方程也无解.
解答 解:去分母得mx=3,
∵x=3时,最简公分母x-3=0,此时整式方程的解是原方程的增根,
∴当x=3时,原方程无解,此时3m=3,解得m=1,
当m=0时,整式方程无解
∴m的值为1或0时,方程无解.
故答案为:1或0.
点评 本题考查了分式方程无解的情况,分式方程无解时,既要考虑分式方程有增根的情形,又要考虑整式方程无解的情形.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
15.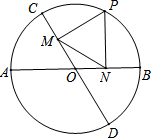 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )| A. | 随P点运动而变化,最大值为$\sqrt{3}$ | B. | 等于$\sqrt{3}$ | ||
| C. | 随P点运动而变化,最小值为$\sqrt{3}$ | D. | 随P点运动而变化,没有最值 |
12.下列计算正确的是( )
| A. | (m+n)2=m2+n2 | B. | m2•m3=m5 | C. | 2m+3n=5mn | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3 |
12.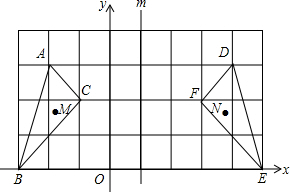 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )| A. | -a | B. | -a+1 | C. | a+2 | D. | -a+2 |
13.记S(n)为非负整数n的各个数位上的数字之和,如S(0)=0,S(1)=1,S(1995)=1+9+9+5=24.则S(1)+S(2)+S(3)+…+S(2015)=( )
| A. | 28097 | B. | 28098 | C. | 28077 | D. | 28087 |
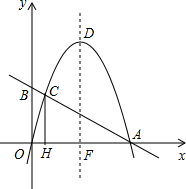 如图,二次函数y=-x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足H,设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
如图,二次函数y=-x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足H,设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.