题目内容
2.已知分式方程$\frac{{x}^{2}+1}{x}$+$\frac{2x}{{x}^{2}+1}$=3,如果t=$\frac{{x}^{2}+1}{x}$,那么原方程可化为关于t的整式方程是t2-3t+2=0.分析 把t=$\frac{{x}^{2}+1}{x}$代入方程,得出t+$\frac{2}{t}$=3,整理成一般形式即可.
解答 解:∵$\frac{{x}^{2}+1}{x}$+$\frac{2x}{{x}^{2}+1}$=3,t=$\frac{{x}^{2}+1}{x}$,
∴t+$\frac{2}{t}$=3,
整理得:t2-3t+2=0,
故答案为:t2-3t+2=0.
点评 本题考查了用换元法解分式方程的应用,解此题的关键是能正确换元,题目是一道比较典型的题目,难度不是很大.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
12.在圆中,45°的圆周角所对的弦长为4$\sqrt{2}$,则圆的半径为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.下列命题,正确的是( )
| A. | 所有正方形都全等 | |
| B. | 等腰梯形的对角线互相平分 | |
| C. | 相等的圆周角所对的弧相等 | |
| D. | 顺次连结四边形各边中点所得到的四边形是平行四边形 |
 如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).
如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).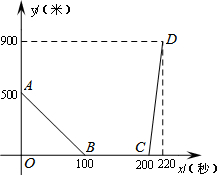 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,