题目内容
13．记S（n）为非负整数n的各个数位上的数字之和，如S（0）=0，S（1）=1，S（1995）=1+9+9+5=24．则S（1）+S（2）+S（3）+…+S（2015）=（ ）| A． | 28097 | B． | 28098 | C． | 28077 | D． | 28087 |
分析 不妨先求0～1999的所有数字之和，再求2000～2015的所有数字之和，将数配对，1与1998一对，2与1997一对…994与995一对，1999一对．共1000对，每对的数字和为1+9+9+9=28；2000～2015的所有数字之和为2×18+1×8+3×2+4×2+5×2+6+7+8+9=98．
解答 解 （1+9×3）×（2000÷2）
=28×1000
=28000，
2×18+1×8+3×2+4×2+5×2+6+7+8+9=98
=28000+98
=28098
所以S（1）+S（2）+S（3）+…+S（2015）=28098．
故选：B．
点评 此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4．
如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=$\frac{1}{2}$DM，HN=2NE，HC与NM的延长线交于点P，则tan∠NPH的值为（ ）
如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=$\frac{1}{2}$DM，HN=2NE，HC与NM的延长线交于点P，则tan∠NPH的值为（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
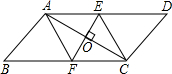已知：如图，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别相交于点E、F．求证：四边形AFCE是菱形．
18．
关于x的一元一次不等式组的解集在数轴上表示如图所示，则该不等式组的解集是（ ）
关于x的一元一次不等式组的解集在数轴上表示如图所示，则该不等式组的解集是（ ）| A． | x＜-3 | B． | x≤-3 | C． | x＜-1 | D． | x≤-1 |
如图，在6×6的正方形网格中，每个小正方形的面积都等于1，以格点为顶点，画一个面积为13的三角形．
如图，已知A（-4，n），B（2，-4）是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点，则不等式kx+b-$\frac{m}{x}$＜0的解集为-4＜x＜0或x＞2．
