Question

14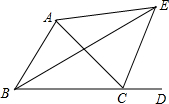．如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠CAE=50°，求∠BEC的度数．

Answer 1

分析 过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，求出∠CAH的度数，求出∠BAC，根据三角形的外角性质求出∠BAC=2∠BEC，即可求出答案．

解答 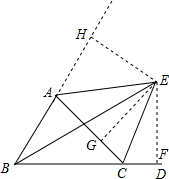解：过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，
∵△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，
∴EH=EF，EG=EF，
∴EH=EG，
∴AE是∠CAH的平分线，
∵∠CAE=50°，
∴∠CAH=100°，
∴∠BAC=80°，
∵BE平分∠ABC，CE平分∠ACD，
∴∠ACD=2∠ECD，∠ABC=2∠EBC，
∵∠ECD=∠BEC+∠EBC，∠ACD=∠ABC+∠BAC，
∴∠BAC=2∠BEC，
∴∠BEC=$\frac{1}{2}$∠BAC=40°．

点评 本题考查了三角形外角性质，角平分线性质的应用，主要考查学生运用性质进行推理的能力．