题目内容
6．两个二次函数y=ax2+bx+c与y=bx2+ax+c在同一平面直角坐标系中的图象只可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据抛物线对称轴和抛物线与y轴的交点坐标进行判断．
解答 解：由函数y=ax2+bx+c与y=bx2+ax+c知，这两个抛物线与y轴的交点相同．故排除C选项；
由函数y=ax2+bx+c与y=bx2+ax+c知，这两个抛物线的对称轴x=-$\frac{b}{2a}$与x=-$\frac{a}{2b}$的符号相同，即这两条对称轴在y轴的同侧，故排除A、B选项．
故选：D．
点评 本题考查了二次函数的图象．熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标以及抛物线与坐标轴的交点等．
练习册系列答案
阅读快车系列答案
相关题目
17．不等式（a-1）x＞1的解集是x＞$\frac{1}{a-1}$，则a的取值范围是（ ）
| A． | a＞1 | B． | a＜1 | C． | a≠0 | D． | 以上都不对 |
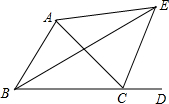如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠CAE=50°，求∠BEC的度数．
如图，已知AB，CD相交于O，△ACO≌△BDO，AE=BF，求证：CE=FD．
15．在实数-2，0，$\frac{1}{2}$，-π中，最小的一个实数是（ ）
| A． | -2 | B． | 0 | C． | $\frac{1}{2}$ | D． | -π |
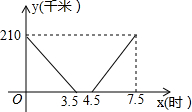甲、乙两地相距210千米，一辆货车将货物由甲地运至乙地，卸载后返回甲地．若货车距乙地的距离y（千米）与时间t（时）的关系如图所示，根据所提供的信息，回答下列问题：