题目内容
9. 如图,已知△ABC为等边三角形,延长BC到点D,延长BA到点E,使AE=BD,连结CE和DE.求证:△CDE为等腰三角形.
如图,已知△ABC为等边三角形,延长BC到点D,延长BA到点E,使AE=BD,连结CE和DE.求证:△CDE为等腰三角形.
分析 要证明△CDE为等腰三角形,只要证明EC=ED,作辅助线,延长BD至F,使DF=BC,连接EF,可以证明△ECB≌△EDF,从而可以证明结论成立.
解答  证明:延长BD至F,使DF=BC,连接EF,如右图所示,
证明:延长BD至F,使DF=BC,连接EF,如右图所示,
∵AE=BD,△ABC为等边三角形,
∴BE=BF,∠B=60°,
∴△BEF为等边三角形,
∴∠F=60°,
∴BE=EF,∠B=∠F=60°,BC=DF,
∴△ECB≌△EDF(SAS),
∴EC=ED,
即△CDE为等腰三角形.
点评 本题考查等腰三角形的判定与性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
17.不等式(a-1)x>1的解集是x>$\frac{1}{a-1}$,则a的取值范围是( )
| A. | a>1 | B. | a<1 | C. | a≠0 | D. | 以上都不对 |
 如图:在△ABC中,AB=5,AC=4,P是AB上一点,且AP=3,若Q在AC上,试确定Q点的位置,使以A、P、Q为顶点的三角形与△ABC相似.
如图:在△ABC中,AB=5,AC=4,P是AB上一点,且AP=3,若Q在AC上,试确定Q点的位置,使以A、P、Q为顶点的三角形与△ABC相似. 已知二次函数的图象如图所示,求这个二次函数的解析式.
已知二次函数的图象如图所示,求这个二次函数的解析式.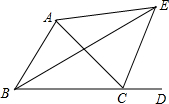 如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=50°,求∠BEC的度数.
如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=50°,求∠BEC的度数.