题目内容
19.抛物线过(1,0),(3,0),交y轴于(0,3),则此抛物线的解析式是y=-x2+2x+3.分析 设其解析式为交点式用待定系数法求得二次函数的解析式.
解答 解:∵抛物线过A(-1,0)和B(3,0)两点
设抛物线的解析式为y=a(x+1)(x-3).
∵交y轴于(0,3),
3=a×(0+1)(0-3),
a=-1.
故抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3,
即y=-x2+2x+3,
故答案为y=-x2+2x+3.
点评 在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写表格:
(2)根据这5次成绩,你认为推荐谁参加射击比赛更合适,请说明理由.
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写表格:
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 8 | 0.4 |
| 乙 | 8 | 9 | 9 | 3.2 |
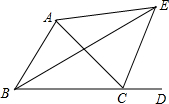 如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=50°,求∠BEC的度数.
如图,△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E,若∠CAE=50°,求∠BEC的度数. 如图,已知AB,CD相交于O,△ACO≌△BDO,AE=BF,求证:CE=FD.
如图,已知AB,CD相交于O,△ACO≌△BDO,AE=BF,求证:CE=FD.