题目内容
5.已知[x]表示不超过x的最大整数,例如[2]=2,[2.9]=2,设f(x)=[x[x]],(1)当1≤x<2时,则f(x)的值等于1,f(x)的值的个数是1;
(2)当1≤x<3时,则f(x)的值等于1,4,5,f(x)的值的个数是3;
(3)当1≤x<n时,求f(x)的值的个数.
分析 (1)由[x]表示不超过x的最大整数,可求得当1≤x<2时,[x[x]]的值,继而求得答案;
(2)由[x]表示不超过x的最大整数,可求得当1≤x<3时,[x[x]]的值,继而求得答案;
(3)由[x]表示不超过x的最大整数,可求得当1≤x<n时,[x[x]]的值,继而求得答案.
解答 解:(1)∵当1≤x<2时,[x]=1,1≤x[x]<2,
∴[x[x]]=1,
即f(x)=1,f(x)的值的个数是1;
故答案为:1,1;
(2)∵当1≤x<3时,[x]=1或2,x[x]=1,或4≤x[x]<6,
∴[x[x]]=1,4,5,
即f(x)=1,4,5,f(x)的值的个数是3;
故答案为:1,4,5;3;
(3)当1≤x<n时,[x]=1,2,3…n-1,x[x]=1,或4≤x[x]<6,或9≤x[x]<12,….
∴[x[x]]=1,4,5,9,10,11,16,17,19,…
∴f(x)的值的个数是1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$.
点评 此题考查了取整函数的知识.注意理解[x]表示不超过x的最大整数是关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13.两个连续奇数的平方差一定是( )
| A. | 2的倍数,但不一定是4的倍数 | B. | 4的倍数,但不一定是8的倍数 | ||
| C. | 8的倍数,但不一定是16的倍数 | D. | 16的倍数,但不一定是32的倍数 |
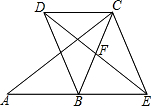 如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD.
如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD.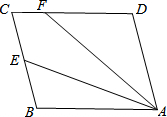 如图,?ABCD中,E是BC边的中点,连接AE,F为CD边上一点,AE平分∠FAB.
如图,?ABCD中,E是BC边的中点,连接AE,F为CD边上一点,AE平分∠FAB.