题目内容
10.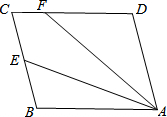 如图,?ABCD中,E是BC边的中点,连接AE,F为CD边上一点,AE平分∠FAB.
如图,?ABCD中,E是BC边的中点,连接AE,F为CD边上一点,AE平分∠FAB.(1)若∠DFA=40°,求∠FAE的度数;
(2)求证:AF=CD+CF.
分析 (1)由CD∥AB得∠DFA=∠FAB,又∠FAE=$\frac{1}{2}$∠DFA,由此即可解决问题.
(2)连接FE,延长FE交AB的延长线于M,作EH⊥AF于H,EK⊥AM于K,先证明△CEF≌△BEM得CF=BM.EF=EM,再证明△EHF≌△EKM得∠EFH=∠EMK,由此即可解决问题.
解答 (1)解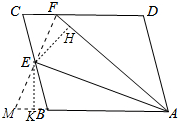 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴CD∥AB,∴∠DFA=∠FAB=40°,
∵∠EAF=∠EAM,
∴∠FAE=$\frac{1}{2}$∠FAB=20°.
(2)证明:连接FE,延长FE交AB的延长线于M,作EH⊥AF于H,EK⊥AM于K,
∵CF∥MB,
∴∠C=∠EBM,
在△CFE和△BME中,
$\left\{\begin{array}{l}{∠C=∠EBM}\\{EC=EB}\\{∠CEF=∠BEM}\end{array}\right.$,
∴△CEF≌△BEM,
∴CF=BM.EF=EM,
∵∠EAH=∠EAK,EH⊥AF,EK⊥AM,
∴EH=EK,
在RT△EHF和RT△EKM中,
$\left\{\begin{array}{l}{EF=EM}\\{EH=EK}\end{array}\right.$,
∴△EHF≌△EKM,
∴∠EFH=∠EMK,
∴AF=AM=BM+AB,
∵四边形ABCD是平行四边形,
∴CD=AB,
∴AF=CD+CF.
点评 本题考查平行四边形的性质、全等三角形的判定和性质,角平分线的性质等知识,添加辅助线是解决问题的关键,中线延长,利用角平分线作辅助线是常用手段,属于中考常考题型.

练习册系列答案
相关题目
15.我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
19.计算$\sqrt{(-2-{x}^{2})^{2}}$的结果是( )
| A. | -2-x2 | B. | 2+x2 | C. | -2+x2 | D. | 2-x2 |
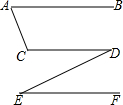 如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.
如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.