题目内容
已知关于x的方程x2+2（3-m）x-6m+3=0（m为常数），证明：不论m取何值，此方程总有两个不相等的实数根．
考点：根的判别式
专题：证明题
分析：求出方程的判别式，证明其总大于0即可．
解答：证明：∵a=1，b=2（3-m），c=-6 m+3，
∴△=b2-4ac=[2（3-m）]2-4×1×（-6 m+3）
=4m2+24＞0，
∴无论m取何值时，此方程总有两个不相等的实数根．
∴△=b2-4ac=[2（3-m）]2-4×1×（-6 m+3）
=4m2+24＞0，
∴无论m取何值时，此方程总有两个不相等的实数根．
点评：本题主要考查一元二次方程根的判别式，掌握一元二次方程的判别式与根的情况是解题的关键．
练习册系列答案
相关题目
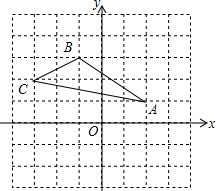如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（2，1），B（-1，3），C（-3，2）．
小颖为学校联欢会设计了一个“配紫色”游戏：下面是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，游戏者同时转动两个转盘，如果两个转盘分别转出了红色和蓝色，那么他就赢了，因为红色和蓝色在一起配成了紫色．