题目内容
3.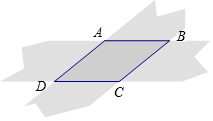 如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为4$\sqrt{2}$.
如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为4$\sqrt{2}$.
分析 过点A作AE⊥BC于E,AF⊥CD于F,首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形;连接AC,BD相较于点O,在直角三角形AOB中利用勾股定理可求出BO的长,进而可求出BD的长.
解答 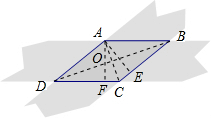 解:过点A作AE⊥BC于E,AF⊥CD于F,
解:过点A作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC•AE=CD•AF.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
连接AC,BD相较于点O,
∴AC⊥BD,AO=$\frac{1}{2}$AC=1,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=2$\sqrt{2}$,
∴BD=2BO=4$\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题考查了菱形的判定与性质、平行四边形的判断和性质以及勾股定理应用,证得四边形ABCD为菱形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.一次函数y=3x-6的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
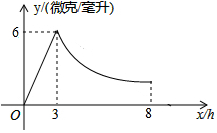 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.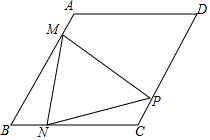 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.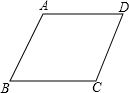 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).
如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).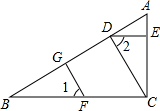 完成下列证明:
完成下列证明: