题目内容
16. 如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )| A. | 11 | B. | 8 | C. | 12 | D. | 3 |
分析 过E作EF⊥BC于F,根据角平分线性质得出EF=DE=3,根据三角形的面积公式求出即可.
解答 解:过E作EF⊥BC于F,
∵CD是AB边上的高线,BE平分∠ABC,DE=3,
∴EF=DE=3,
∴△BCE的面积S=$\frac{1}{2}×BC×EF$=$\frac{1}{2}×8×3=12$,
故选C.
点评 本题考查了角平分线性质的应用,能求出BC边上的高是解此题的关键,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.如图,是作一个角等于已知角的作图痕迹,判断∠A′O′B′=∠AOB的依据是( )
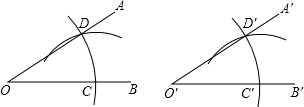

| A. | SSS | B. | SAS | C. | AAS | D. | ASA |
8.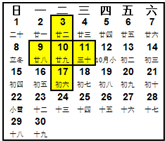 如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为46,则这5个数的和为( )
如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为46,则这5个数的和为( )
 如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为46,则这5个数的和为( )
如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为46,则这5个数的和为( )| A. | 69 | B. | 84 | C. | 115 | D. | 207 |
5.若等腰三角形的一个内角为80°,那么这个等腰三角形的顶角是( )
| A. | 20°或80° | B. | 80° | C. | 40° | D. | 20° |
 如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.
如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.
 颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是12米.
颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是12米.