题目内容
9. 已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.
已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.
分析 首先证明a∥b,可得∠1=∠3=60°,再根据∠2=180°-∠3即可解决问题.
解答 解:∵直线a⊥m,直线b⊥m,
∴a∥b,
∴∠1=∠3=60°,
∴∠2=180°-∠3=120°,
故答案为120°.
点评 本题考查平行线的判定和性质、邻补角的性质等知识,灵活运用知识是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.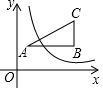 如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
 如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )| A. | 1≤k≤4 | B. | 2≤k≤8 | C. | 2≤k≤16 | D. | 8≤k≤16 |
17.在平面直角坐标系中,一次函数y=x-1的图象是( )
| A. |  | B. |  | C. |  | D. |  |
4.某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示正确的是( )
| A. | 0.69×10-6 | B. | 6.9×10-7 | C. | 69×10-8 | D. | 6.9×107 |
1. 小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
 小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )
小明将图中两水平线l1与l2的其中一条当成x轴,且向右为正方向;两铅垂线l3与l4的其中一条当成y轴,且向上为正方向,并且在此平面直角坐标系上画出二次函数y=-x2-2x+1的图象,则关于他选择x轴与y轴的叙述正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
19. 如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
 如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )
如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线,过点D作DE⊥AB,垂足为E,则下列结论错误的是( )| A. | DE=DC | B. | ∠ADE=∠ABC | C. | BE=BC | D. | ∠ADE=∠ABD |
 以菱形ABCD的对角线交点O为坐标原点,AC所在的直线为x轴,已知A(-4,0),B(0,-2),M(0,4),P为折线BCD上一动点,作PE⊥y轴于点E,设点P的纵坐标为a.
以菱形ABCD的对角线交点O为坐标原点,AC所在的直线为x轴,已知A(-4,0),B(0,-2),M(0,4),P为折线BCD上一动点,作PE⊥y轴于点E,设点P的纵坐标为a. 如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.
如图,⊙O的半径为3,弦AB与弦CD平行,将图中阴影部分沿直线CD折叠后所得圆弧恰与AB相切.若CD=2$\sqrt{5}$,则AB=4$\sqrt{2}$.