题目内容
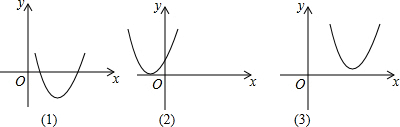
18.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,请根据抛物线在各图中的位置,在以下相应三个问题中的空格中填上序号:①方程y=ax2+bx+c(a≠0)有两个相等的实数根的是(2);
②方程y=ax2+bx+c(a≠0)的△>0的是(1);
③方程y=ax2+bx+c(a≠0)没有实数根的是(3).
分析 根据一元二次方程根的判别式,b2-4ac<0方程没有实数根,b2-4ac=0,方程有两个相等的实数根,b2-4ac>0方程有两个不相等的实数根,即可得出答案.
解答 解:①方程y=ax2+bx+c(a≠0)有两个相等的实数根,则b2-4ac=0,抛物线与x轴只有一个交点,故答案为:(2);
②方程y=ax2+bx+c(a≠0)的△>0,则抛物线与x轴有两个不同的交点,故答案为:(1);
③方程y=ax2+bx+c(a≠0)没有实数根,则抛物线与x轴没有交点,故答案为:(3).
点评 此题主要考查了一元二次方程根情况与二次函数与x轴交点个数的关系,熟练掌握△与0的关系与二次函数与x轴交点个数之间的关系是解决问题的关键.

练习册系列答案
相关题目
13.在数轴上与-3的距离等于4的点表示的数是( )
| A. | 1 | B. | -7 | C. | -1或7 | D. | 1或-7 |
 如图,要建一个面积为130m2的仓库,仓库的一边靠墙(墙长16米),并在与墙平行的一边开一道1米宽的门.现有能围成32米长的木板,求仓库的长和宽.
如图,要建一个面积为130m2的仓库,仓库的一边靠墙(墙长16米),并在与墙平行的一边开一道1米宽的门.现有能围成32米长的木板,求仓库的长和宽. 解不等式组:$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$.把解集在数轴上表示出来,并求出这个等式的整数解.
解不等式组:$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$.把解集在数轴上表示出来,并求出这个等式的整数解.