Question

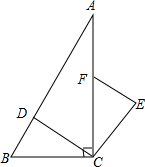如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后的CE，连接EF．当CD⊥AB时，判断EF与CD的位置关系，并说明理由．

Answer 1

考点：旋转的性质

专题：常规题型

分析：由CD⊥AB得∠BDC=90°，再根据旋转的性质得∠DCE=90°，CB=CE，则根据等角的余角相等得∠BCD=∠FCE，再利用“SAS”证明△CBD≌△CFE，所以∠CDB=∠E=90°，然后根据平行线的判定方法得EF∥CD．

解答：解：EF∥CD．理由如下：
∵CD⊥AB，
∴∠BDC=90°，
∵线段CD绕点C按顺时针方向旋转90°后的CE，
∴∠DCE=90°，CB=CE，
即∠DCA+∠FCE=90°，
而∠BCD+∠DCA=90°，
∴∠BCD=∠FCE，
在△CBD和△CFE中，

CB=CE ∠BCD=∠FCE CB=CF

∴△CBD≌△CFE（SAS），
∴∠CDB=∠E=90°，
而∠DCE=90°，
∴EF∥CD．

点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了全等三角形的判定与性质．