题目内容
4.下列各式计算正确的是( )| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $2+\sqrt{2}=2\sqrt{2}$ | C. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ | D. | $\frac{{\sqrt{12}+\sqrt{10}}}{2}=\sqrt{6}+\sqrt{5}$ |
分析 根据二次根式的加减法,即可解答.
解答 解:A、$\sqrt{2}+\sqrt{3}$≠$\sqrt{5}$,故错误;
B、2+$\sqrt{2}$≠2$\sqrt{2}$,故错误;
C、$3\sqrt{2}-\sqrt{2}=2\sqrt{2}$,正确;
D、$\frac{\sqrt{12}+\sqrt{10}}{2}=\frac{2\sqrt{3}+\sqrt{10}}{2}=\sqrt{3}+\frac{\sqrt{10}}{2}$,故错误;
故选:C.
点评 本题考查了二次根式的加减法,解决本题的关键是熟记二次根式的加减法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知一次函数y=(1+2m)x-1中,函数值y随自变量x的增大而减小,那么m取值范围是( )
| A. | m<-$\frac{1}{2}$ | B. | m≥-$\frac{1}{2}$ | C. | m≤-$\frac{1}{2}$ | D. | m>-$\frac{1}{2}$ |
12.下列各式中与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{9}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
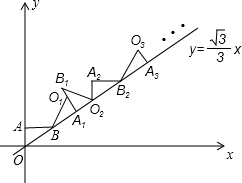 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6.
如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=$\frac{\sqrt{3}}{3}$x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是($\sqrt{3}$,1),则点A8的横坐标是6$\sqrt{3}$+6. 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP