题目内容
9．当m=-9时，关于x的方程x2-6x-m=0有两个相等的实数根．分析 由方程有两根相等的实数根结合根的判别式，即可得出关于m的一元一次方程，解方程即可得出结论．
解答 解：∵关于x的方程x2-6x-m=0有两个相等的实数根，
∴△=（-6）2-4×1×（-m）=36+4m=0，
解得：m=-9．
故答案为：-9．
点评 本题考查了根的判别式，解题的关键是得出△=36+4m=0．本题属于基础题，难度不大，解决该题型题目时，根据方程根的情况结合根的判别式，得出方程（不等式或不等式组）关键．
练习册系列答案
相关题目
19．网络时代的到来，很多家庭都接入了网络，电信局规定了拨号入网两种收费方式，用户可以任选其一；
①某用户某月上网的时间为x小时，两种收费方式的费用分别为yA（元）、yB（元）．写出yA、yB与x之间的函数关系式；
②在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？
①某用户某月上网的时间为x小时，两种收费方式的费用分别为yA（元）、yB（元）．写出yA、yB与x之间的函数关系式；
②在上网时间相同的条件下，请你帮该用户选择哪种方式上网更省钱？
| 月租费（元） | 计费方式（元/分） | |
| A方式 | 0 | 0.05 |
| B方式 | 54 | 0.02 |
如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E，求证：AD=CE．
4．下列各式计算正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $2+\sqrt{2}=2\sqrt{2}$ | C． | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ | D． | $\frac{{\sqrt{12}+\sqrt{10}}}{2}=\sqrt{6}+\sqrt{5}$ |
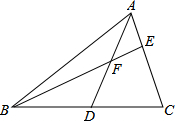如图，在△ABC中，AD为BC边上的中线，E为AC上的一点，BE交AD于点F，已知AE=EF．求证：AC=BF．
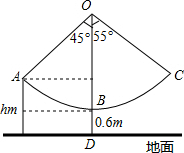某新农村乐园设置了一个秋千场所，如图所示，秋千拉绳OB的长为3m，静止时，踏板到地面距离BD的长为0.6m（踏板厚度忽略不计）．为安全起见，乐园管理处规定：儿童的“安全高度”为hm，成人的“安全高度”为2m（计算结果精确到0.1m）
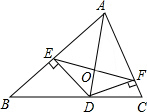如图，在△ABC中，AB=c，AC=b．AD是△ABC的角平分线，DE⊥A于E，DF⊥AC于F，EF与AD相交于O，已知△ADC的面积为1．