题目内容
1.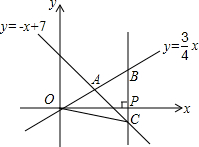 如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象交于点A.
如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象交于点A.(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=$\frac{3}{4}$x和y=-x+7的图象于点B、C,连接OC,若BC=$\frac{5}{7}$OA,求△OBC的面积.
分析 (1)解方程组即可得到结论;
(2)设B(a,$\frac{3}{4}$a),C(a,-a+7),得到BC=$\frac{3}{4}$a-(-a+7)=$\frac{7}{4}$a-7;根据已知条件列方程得到a=$\frac{296}{49}$,于是得到结论.
解答 解:(1)解$\left\{\begin{array}{l}{y=\frac{3}{4}x}\\{y=-x+7}\end{array}\right.$得,$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴A(4,3);
(2)∵过点P作x轴的垂线分别交y=$\frac{3}{4}$x和y=-x+7的图象于点B、C,
∴设B(a,$\frac{3}{4}$a),C(a,-a+7),∴BC=$\frac{3}{4}$a-(-a+7)=$\frac{7}{4}$a-7;
∵OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BC=$\frac{5}{7}$OA,
∴$\frac{7}{4}$a-7=$\frac{5}{7}$×5,
∴a=$\frac{296}{49}$,
∴S△OBC=$\frac{1}{2}×$$\frac{25}{7}$×$\frac{296}{49}$=$\frac{3700}{343}$.
点评 本题考查了两直线平行与相交,二元一次方程组的解法,三角形的面积的计算,正确的理解题意是解题的关键.

练习册系列答案
相关题目
12.下列四个点,在正比例函数y=$\frac{2}{5}$x的图象上的点是( )
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
16.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(x+1)^{2}}$=x+1 | D. | $\sqrt{-4x}$=$\sqrt{-4}\sqrt{x}$ |
13.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间的关系如表,下列说法不正确的是( )
| x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
| A. | x与y都是变量,且x是自变量,y是x的函数 | |
| B. | 弹簧不挂重物时的长度为0cm | |
| C. | 物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 所挂物体质量为7kg时,弹簧长度为23.5cm |
11.若关于x的不等式ax-b>0的解集为x<$\frac{1}{3}$,则关于x的不等式(a+b)x>a-b的解集为( )
| A. | x<-$\frac{1}{2}$ | B. | x$>-\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
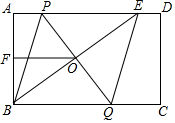 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.