题目内容
13.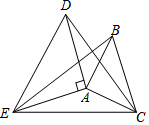 如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )
如图,△ABC和△ADE都是等腰直角三角形,∠EAD=∠BAC=90°,∠DAB=45°,连接BE,DC,EC,则下列说法正确的有( )①BE=DC②AD∥BC③BE=DE④BE=EC.
| A. | ①③ | B. | ②④ | C. | ①②④ | D. | ①②③④ |
分析 由等腰直角三角形的性质得出AE=AD,AB=AC,求出∠EAB=∠DAC=135°,由SAS证明△ABE≌△ACD,得出①正确;证出∠ADC=∠BCD得出②正确;证出∠EAB=∠EAC=135°,由SAS证明△ABE≌△ACE,得出BE=CE,④正确;没有条件能证出BE=DE,③不一定正确;即可得出结论.
解答 解:∵△ABC和△ADE都是等腰直角三角形,
∴AE=AD,AB=AC,
∵∠EAD=∠BAC=90°,∠DAB=45°,
∴∠EAB=∠DAC=135°,
在△ABE与△ACD中$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD(SAS),
∴BE=DC,①正确;
∵∠ADC+∠ACD=∠ACD+∠BCD=45°,
∴∠ADC=∠BCD
∴AD∥BC,②正确;
∵∠EAD=∠BAC=90°,∠DAB=45°,
∴∠EAB=∠EAC=135°,
在△ABE和△ACE中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠EAB=∠EAC}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△ABE≌△ACE(SAS),
∴BE=CE,④正确;
没有条件能证出BE=DE,③不一定正确;
故选:C.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,平行线的判定等知识;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
6. 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
 图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )| A. | 体育场离张强家2.5千米 | |
| B. | 张强在体育场锻炼了15分钟 | |
| C. | 体育场离早餐店4千米 | |
| D. | 张强从早餐店回家的平均速度是$\frac{18}{7}$千米/小时 |
