��Ŀ����
7�� ��ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy��������-M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1��
��ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy��������-M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1����1���ֱ��жϺ���y=$\frac{1}{x}$��x��0����y=x+1��-4��x��2���Dz����н纯���������н纯��������߽�ֵ��
��2��������y=-x+1��a��x��b��b��a���ı߽�ֵ��2����������������ֵҲ��2����b��ȡֵ��Χ��
��3��������y=x2��-1��x��m��m��0����ͼ������ƽ��m����λ���õ��ĺ����ı߽�ֵ��t����m��ʲô��Χʱ������$\frac{3}{4}$��t��1��
���� ��1�������н纯���Ķ��弴�ɵó�����y=$\frac{1}{x}$ ��x��0�������н纯��������y=x+1��-4��x��2�����н纯�����ٴ���x=-4��x=2���ɵó���߽�ֵ��
��2������һ�κ��������ʿɵó�����y=-x+1�ǵ�����������Ϻ��������ֵΪ2���ɵó�a��ֵ���ٴ���b��ֵ����н纯���Ķ����Լ��ú����ı߽�ֵ���ɵó�����b��һԪһ�β���ʽ�飬�ⲻ��ʽ�鼴�ɵó�b��ȡֵ��Χ��
��3����m��1ʱ������x=0���ɵó�y=-m����$\frac{3}{4}$��t��1�ɵó�������������ڣ��Ӷ��ó�m��1����϶��κ����������Լ����κ���ͼ���ϵ�����������ҳ�ԭ����������Ϊ-1��0ʱ��y��ֵ������ƽ�Ƶ����ʼ��ɵó�ƽ�ƺ�ĺ�������ֵ�������н纯���Ķ����Լ���߽�ֵ$\frac{3}{4}$��t��1�����ɵó�����m��һԪһ�β���ʽ�飬�ⲻ��ʽ�鼴�ɵó�m��ȡֵ��Χ������ý⣮
��� �⣺��1�������н纯���Ķ���֪������y=$\frac{1}{x}$ ��x��0�������н纯����
����y=x+1��-4��x��2�����н纯����
��-4+1=-3��2+1=3��
��y=x+1��-4��x��2���߽�ֵΪ3��
��2����k=-1��0��
�ຯ��y=-x+1��ͼ����y��x���������С��
�൱x=aʱ��y=-a+1=2��
��ã�a=-1��
��x=bʱ��y=-b+1��
��$\left\{\begin{array}{l}{-2��-b+1��2}\\{b��a}\\{a=-1}\end{array}\right.$��
��-1��b��3��
��3����m��1����������ƽ��m����λ��x=0ʱ������ֵС��-1��
��ʱ�����ı߽�t��1�������ⲻ������m��1��
��x=-1ʱ��y=1������y=x2���㣨-1��1����
��x=0ʱ��y��С=0������y=x2���㣨0��0����
������ƽ��m����λ������y=x2-m���㣨-1��1-m������0��-m����
��$\frac{3}{4}$��t��1��
��$\left\{\begin{array}{l}{\frac{3}{4}��1-m��1}\\{m��1-m}\end{array}\right.$��$\left\{\begin{array}{l}{-1��-m��-\frac{3}{4}}\\{1-m��m}\end{array}\right.$��
��ã�0��m��$\frac{1}{4}$ �� $\frac{3}{4}$��m��1��
�ʵ�0��m��$\frac{1}{4}$ �� $\frac{3}{4}$��m��1ʱ������$\frac{3}{4}$��t��1��
���� ���⿼����һ�κ��������ʡ����κ��������ʡ��н纯���Ķ����Լ���һԪһ�β���ʽ�飬����Ĺؼ��ǣ���1�������н纯���Ķ����ж�һ�������Ƿ�Ϊ�н纯������2���ҳ�����b��һԪһ�β���ʽ�飻��3���ҳ�����m��һԪһ�β���ʽ�飮���������е��⣬�ѶȲ������������Ŀʱ�������н纯���Ķ����ϱ߽�ֵ�ҳ�����ʽ���ǹؼ���

| 3 | a | b | c | -1 | 2 | �� |
| A�� | -1 | B�� | 0 | C�� | 2 | D�� | 3 |
| A�� | $\frac{3{a}^{4}{b}^{2}}{6{a}^{2}{b}^{4}}$=$\frac{{a}^{3}}{2{b}^{2}}$ | B�� | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | ||
| C�� | $\frac{x+3}{{x}^{2}-9}$=$\frac{3}{x-3}$ | D�� | $\frac{b-a}{��a-b��^{2}}$=$\frac{1}{b-a}$ |
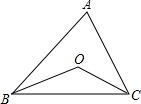 ��֪�ڡ�ABC�У���A=62�㣬BO��CO�ֱ��ǡ�ABC����ACB��ƽ���ߣ���BO��CO�ཻ��O�����BOC�Ķ�����121�㣮
��֪�ڡ�ABC�У���A=62�㣬BO��CO�ֱ��ǡ�ABC����ACB��ƽ���ߣ���BO��CO�ཻ��O�����BOC�Ķ�����121�㣮