题目内容
17.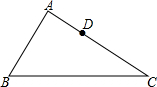 如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
分析 先计算出AD=5,由于△ADE与△ABC有公共角∠A,则根据两组对应边的比相等且夹角对应相等的两个三角形相似,当$\frac{AD}{AC}$=$\frac{AE}{AB}$时,△ADE∽△ACB或当$\frac{AD}{AB}$=$\frac{AE}{AC}$时,△ADE∽△ABC,然后分别利用比例性质计算对应的AE的长.
解答 解:∵AC=15,
∴CD=$\frac{2}{3}$AC=10,
∴AD=AC-CD=5, ∵∠DAE=∠CAB,
∵∠DAE=∠CAB,
∴当$\frac{AD}{AC}$=$\frac{AE}{AB}$时,△ADE∽△ACB,即$\frac{5}{15}$=$\frac{AE}{12}$,解得AE=4;
当$\frac{AD}{AB}$=$\frac{AE}{AC}$时,△ADE∽△ABC,即$\frac{5}{12}$=$\frac{AE}{15}$,解得AE=$\frac{25}{4}$.
答:AE的长为4或$\frac{25}{4}$.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.注意分类讨论思想的运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.若其中一个控制电灯的开关坏了(不知是哪一个),则任意按下两个开关,正好一盏灯亮和一个吊扇转的概率是$\frac{1}{3}$.
如图,某教室的开关控制板上有四个外形完全相同的开关,其中两个分别控制A、B两盏电灯,另两个分别控制C、D两个吊扇.已知电灯、吊扇均正常,且处于不工作状态,开关与电灯、电扇的对应关系未知.若其中一个控制电灯的开关坏了(不知是哪一个),则任意按下两个开关,正好一盏灯亮和一个吊扇转的概率是$\frac{1}{3}$.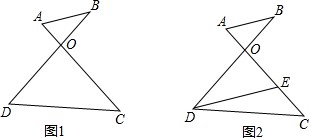 如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.
如图,线段AC与BD交于点O,且AO=3,BO=5,AC=18,OD=9.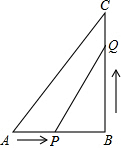 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒: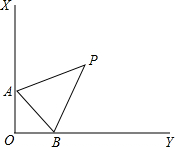 如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.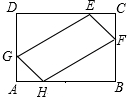 如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.
如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.