题目内容
12.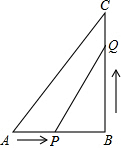 如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:
如图所示,△ABC中,AB=6cm,BC=8cm,∠B=90°,点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果p、Q分别从A、B同时出发,移动了t秒:(1)请用含t的代数式分别表示PB、BQ的长;
(2)当t为何值时,△PBQ的面积等于8cm2?
分析 (1)根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长即可;
(2)设经过t秒钟,△PBQ的面积等于8cm2,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解.
解答 解:(1)p、Q分别从A、B同时出发,移动了t秒,则PB=AB-AP=6-t,BQ=2t;
(2)设经过t秒钟,△PBQ的面积等于8cm2,则
$\frac{1}{2}$(6-t)×2t=8,
整理得:t2-6t+8=0,
解得:t=2或t=4.
答:2或4秒后△PBQ的面积等于8cm2 .
点评 此题主要考查了一元二次方程的应用,找到关键描述语“△PBQ的面积等于8cm2”,得出等量关系是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
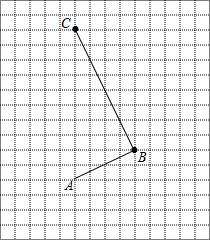 如图,网格中每一个小正方形的边长为1个单位长度.
如图,网格中每一个小正方形的边长为1个单位长度.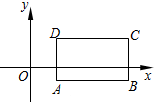 如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).
如图,在平面直角坐标系中,已知长方形ABCD的两个的坐标为A(2,-1),C(8,3).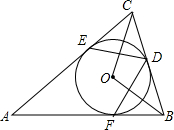 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.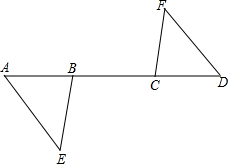 已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF.
已知:如图,A,B,C,D四点在一条直线上,AC=BD,AE∥DF,∠ABE=∠DCF,求证:△ABE≌△DCF.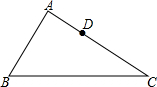 如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.