Question

20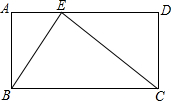．如图，∠A=∠D=90°，AB=CD=12cm，AD=BC=25cm，点E是AD上一点，且AE=9cm，连接BE，CE．判断∠BEC的锐角、钝角还是直角，并说明理由．

Answer 1

分析 首先利用勾股定理求得BE²和EC²，利用勾股定理的逆定理判断△BCE是直角三角形即可判断．

解答 解：∵矩形ABCD中，AD=BC=25cm，
又∵AB=CD=12cm，AE=9cm，
∴ED=16，
∵在直角△ABE中，BE²=AB²+AE²=12²+9²=225，
在直角△CDE中，CE²=CD²+ED²=12²+16²=400，
又∵BC²=25²=625，
∴BC²=BE²+EC²，
∴△BCE是直角三角形，∠BEC=90°

点评 本题考查了勾股定理和勾股定理的逆定理，正确理解定理是解决本题的关键．