题目内容
8. 如图,EQ、FQ分别是∠MEF和∠NFE的平分线,交点是Q,BP、CP分别是∠MBC和∠NCB的平分线,交点是P,F、C在AN上,B、E在AM上.如果∠Q=68°,求∠P的度数.
如图,EQ、FQ分别是∠MEF和∠NFE的平分线,交点是Q,BP、CP分别是∠MBC和∠NCB的平分线,交点是P,F、C在AN上,B、E在AM上.如果∠Q=68°,求∠P的度数.
分析 根据角平分线的定义和三角形内角和定理用∠A表示∠Q和∠P,得到∠Q和∠P的关系,得到答案.
解答 解:∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=$\frac{1}{2}$∠NFE,∠QEF=$\frac{1}{2}$∠MEF,
∴∠Q=180°-$\frac{1}{2}$∠NFE-$\frac{1}{2}$∠MEF
=180°-$\frac{1}{2}$(∠NFE+∠MEF)
=180°-$\frac{1}{2}$(360°-∠AFE-∠AEF)
=180°-$\frac{1}{2}$(180°+∠A)
=90°-$\frac{1}{2}$∠A=68°,
同理,∠P=90°-$\frac{1}{2}$∠A=68°.
点评 本题考查的是角平分线的定义和三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19.不等式组$\left\{\begin{array}{l}{x+2>0}\\{2-x>-1}\end{array}\right.$的非负整数解为( )
| A. | 0,1,2,3 | B. | 0,1,2 | C. | -1,1,2,3 | D. | 1,2,3 |
18. 如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )
如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )
 如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )
如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )| A. | 1cm,1cm,1cm | B. | 1.5cm,1.5cm,1.5cm | ||
| C. | 2cm,2cm,2cm | D. | 2cm,1.5cm,1cm |
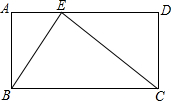 如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由.
如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由.