题目内容
18.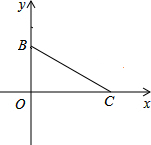 如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.
如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.
分析 由B(0,3),C(4,0),得到OB=3,OC=4,BC=$\sqrt{{OB}^{2}{+OC}^{2}}$=5,当AB=BC=5时,OA=OC=4,得到A1(-4,0),当AB=AC时,由勾股定理得到A2($\frac{7}{8}$,0),当AC=BC=5时,得到OA3=9,得到A3(9,0),
解答 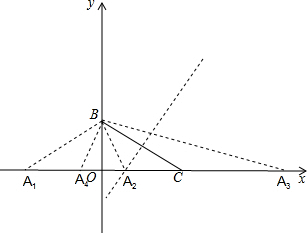 解:∵B(0,3),C(4,0),
解:∵B(0,3),C(4,0),
∴OB=3,OC=4,
∴BC=$\sqrt{{OB}^{2}{+OC}^{2}}$=5,
当AB=BC=5时,OA=OC=4,
∴A1(-4,0),
当AB=AC时,
${{OA}_{2}}^{2}$+OB2=${{BA}_{2}}^{2}$,
∴OA2=$\frac{7}{8}$,
∴A2($\frac{7}{8}$,0),
当AC=BC=5时,
∴OA3=9,OA4=-1,
∴A3(9,0),A4(-1,0).
综上所述:点A的坐标为(-4,0),($\frac{7}{8}$,0),(9,0),(-1,0).
点评 本题主要考查了等腰三角形的判定,线段垂直平分线的性质,勾股定理得应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.同一副三角板(两块)画角,不可能画出的角的度数是( )
| A. | 135° | B. | 75° | C. | 55° | D. | 15° |
7.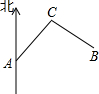 如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
 如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )
如图,我国鱼政救助船在海上自南向北航行,同时,一艘鱼船从B港出发沿北偏西60°方向航行,t小时后,鱼政救助船到达A处,鱼船到达C处,此时鱼政救助船测得该鱼船在北偏东40°方向,则此时鱼船观测港口与鱼政救助船的视角∠ACB为( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
8.下列不等式中,属于一元一次不等式的是( )
| A. | 4>1 | B. | 3x-2<4 | C. | $\frac{1}{x}$<2 | D. | 4x-3<2y-7 |

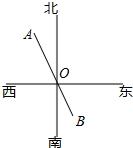 如图,A、O、B在同一条直线上,如果OA的方向是北偏西37°47′,那么OB的方向是南偏东37°47′.
如图,A、O、B在同一条直线上,如果OA的方向是北偏西37°47′,那么OB的方向是南偏东37°47′.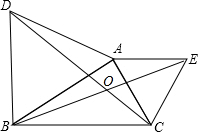 如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.
如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°. 如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.
如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.