题目内容
3.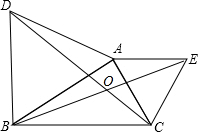 如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.
如图,△ABD,△AEC都是等边三角形,BE交CD于点O,则∠DOE=120°.
分析 先证∠DAC=∠BAE,再证明△DAC≌△BAE,得出对应角相等∠ADC=∠ABE,再由三角形的外角关系即可得出结果.
解答 解:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠DAC=∠BAE}&{\;}\\{AC=AE}&{\;}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
∴∠DPE=∠BDP+∠DBP
=∠BDP+∠DBA+∠ABE
=∠BDP+∠ADC+∠DBA
=60°+60°
=120°.
点评 本题考查了等边三角形的性质、三角形的外角性质、全等三角形的判定与性质;熟练掌握三角形全等的判定方法证明三角形全等是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.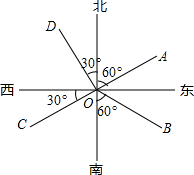 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )
 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
8.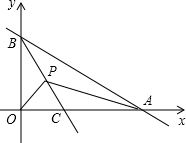 如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
 如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )
如图,A、B分别为x轴,和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动,设△APB和△OPB的面积为S1,S2,则$\frac{S_1}{S_2}$等于( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
12.世界第一高峰珠穆朗玛峰,其海拔约8844.43米,是一条近似东西向的弧形山系,近似数8844.43用科学记数法精确到十位,其中正确的是( )
| A. | 88.4×102 | B. | 8.84×103 | C. | 8.80×103 | D. | 8.8×103 |
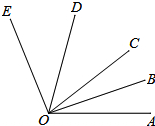 如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.
如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.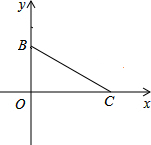 如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.
如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.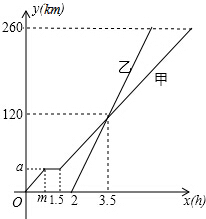 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶$\frac{1}{4}$或$\frac{11}{4}$小时后,两车恰好相距50km.
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶$\frac{1}{4}$或$\frac{11}{4}$小时后,两车恰好相距50km.