题目内容
11.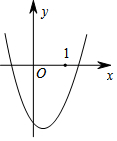 一抛物线的图象如图所示,则下列结论中,正确的是( )
一抛物线的图象如图所示,则下列结论中,正确的是( )| A. | a<0 | B. | ab>0 | C. | ac>0 | D. | 2a+b>0 |
分析 根据二次函数开口向上判断出a>0,再根据对称轴判断出b>0,再根据与y轴的交点判断出c<0;根据对称轴列出不等式求解即可得到2a+b>0.
解答 解:∵二次函数开口向上,
∴a>0,
∴A错误;
∵对称轴在y轴左边,
∴-$\frac{b}{2a}$>0,
∴b<0,
∴ab<0,
∴B错误;
∵二次函数图象与y轴的交点在y轴负半轴,
∴c<0,
∴ac<0,
∴C错误;
∵$-\frac{b}{2a}<1$
∴$\frac{b}{2a}>-1$,
∵a>0,
∴b>-2a,
∴b+2a>0
∴D正确.
故选D.
点评 本题考查了二次函数图象与系数的关系,关键是利用了二次函数的开口方向,对称轴,与y轴的交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列命题的逆命题正确的是( )
| A. | 全等三角形对应角相等 | B. | 对顶角相等 | ||
| C. | 全等三角形对应边相等 | D. | 若a=b,则|a|=|b| |
16.不等式2x-1<3的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
1.-$\frac{3}{4}$的相反数是( )
| A. | $-\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-|{\frac{3}{4}}|$ |
 将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切?
将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切? 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.