题目内容
8.先化简再求值(1)(x+3)2+(x+2)(x-2)-4x(x+13),其中x2+3x=2.
(2)(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=$\frac{1}{2}$,b=-1.
分析 (1)先算乘法,再合并同类项,求出x得值代入即可;
(2)先算乘法和除法,再合并同类项,最后代入求出即可.
解答 解:(1)(x+3)2+(x+2)(x-2)-4x(x+13)
=x2+6x+9+x2-4-4x2-52x
=-2x2-46x+5,
∵x2+3x=2,
∴x2=2-3x,x=$\frac{-3±\sqrt{17}}{2}$,
当x=$\frac{-3+\sqrt{17}}{2}$时,原式=-2(2-3x)-46x+5=1-40x=61-20$\sqrt{17}$;
当x=$\frac{-3-\sqrt{17}}{2}$时,原式=-2(2-3x)-46x+5=1-40x=61+20$\sqrt{17}$;
(2)(a2b-2ab2-b3)÷b-(a+b)(a-b)
=a2-2ab-b2-a2+b2
=-2ab,
当a=$\frac{1}{2}$,b=-1时,原式=-2×$\frac{1}{2}$×(-1)=1.
点评 本题考查了整式的化简求值和解一元二次方程的应用,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.△ABC绕点A按顺时针时方向旋转了60°,得到△AEF,则下列结正确是( )
| A. | ∠BAE=60° | B. | EF=BC | C. | AC=AF | D. | ∠EAF=60° |
3.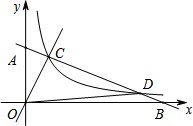 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
 如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )
如图,在平面直角坐标系中,直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点,已知直线OC解析式为y=2x,S△AOD=6,则D点的坐标为( )| A. | $(3,\frac{2}{3})$ | B. | $(4,\frac{1}{2})$ | C. | $(5,\frac{2}{5})$ | D. | $(6,\frac{1}{3})$ |
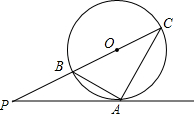 如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.
如图,P为⊙0外一点,A为⊙0上一点,直线OP交⊙0于B、C,连接AB、AC,且∠PAB=∠C.