题目内容
8.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,若CD=18,AD=24,则tanB=$\frac{4}{3}$.分析 根据同角的余角相等,可得tanB=tan∠CAD,再根据正切函数的定义即可求解.
解答  解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,
解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,
∴∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴tanB=tan∠ACD=$\frac{AD}{CD}$.
∵CD=18,AD=24,
∴tanB=$\frac{24}{18}$=$\frac{4}{3}$.
故答案为$\frac{4}{3}$.
点评 此题主要考查了解直角三角形的能力.关键是找出∠B=∠ACD,会利用三角函数的定义求值.

练习册系列答案
相关题目
16.下列各式中正确的是( )
| A. | sin35°+sin45°=sin80° | B. | cos30°+cos15°=cos45° | ||
| C. | tan60°+cos22°=tan82° | D. | tan30°=$\frac{sin30°}{cos30°}$ |
3.在Rt△ABC中,∠C=90°,BC=a,AC=b,且3a=4b,则∠A的度数为( )
| A. | 53.48° | B. | 53.13° | C. | 53.13′ | D. | 53.48′ |
18.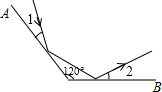 如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
 如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
 在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案. 如图①、②分别表示甲、乙两个楼梯.
如图①、②分别表示甲、乙两个楼梯.