题目内容
8．若⊙O的半径为5，圆心O的坐标为（3，4）．点P的坐标为（5，2），则P与点⊙O的位置关系是（ ）| A． | 点P在⊙O内 | B． | 点P在⊙O上 | C． | 点P在⊙O外 | D． | 不能确定 |
分析 根据勾股定理，可得点与圆心的距离，根据则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．
解答 解：由勾股定理，得
OP=$\sqrt{（5-3）^{2}+（2-4）^{2}}$=2$\sqrt{2}$＜5，
点P在⊙O内，
故选：A．
点评 本题考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
相关题目
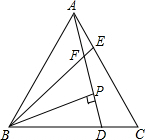如图，已知△ABC为等边三角形，AE=CD，AD、BE相交于点F．
某养猪专业户利用一堵砖墙（长度足够）围成一个长方形猪栏，围猪栏的栅栏一共长40m，设这个长方形的相邻两边的长分别为x（m）和y（m）．
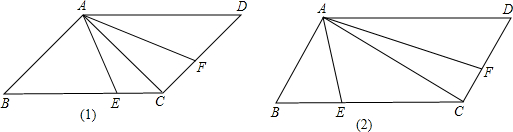
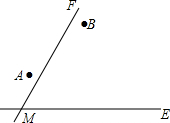两城镇A、B与两条公路ME、MF位置如图所示，现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME、MF的距离也必须相等，且在∠FME的内部，那么点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）
如图，已知A（1，3），B（5，0），在x轴上是否存在点P，使△PAB为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
如图，AD，BE，CF是△ABC的高，K，M，N分别为△AEF，△BFD，△CDE的垂心，求证：△DEF≌△KMN．