题目内容
20. 如图,已知A(1,3),B(5,0),在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
如图,已知A(1,3),B(5,0),在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 过A作AC⊥x轴于C,根据A(1,3),B(5,0),得到AC=3,BC=4,根据勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,①若AP=AB=5,则PC=BC=4,求得 P1(-3,0);②若BP=BA=5,求得P2(0,0);③若PA=PB,则P在AB的垂直平分线上,求得P3($\frac{25}{8}$,0);④若BA=PB=5,求得P4(10,0).
解答  解:存在,
解:存在,
过A作AC⊥x轴于C,
∵A(1,3),B(5,0),
∴AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
①若AP=AB=5,则PC=BC=4,
∴P1(-3,0);
②若BP=BA=5,则P2(0,0);
③若PA=PB,则P在AB的垂直平分线上,
∴$\frac{PB}{5}=\frac{\frac{5}{2}}{4}$,
∴PB=$\frac{25}{8}$,
∴P3($\frac{25}{8}$,0);
④若BA=PB=5,则P4(10,0).
综上所述:p(-3,0),(0,0),($\frac{25}{8}$,0),(10,0).
点评 本题主要考查了等腰直角三角形的判定和性质,勾股定理,相似三角形的判定和性质,分类讨论是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.方程x2=1的解是( )
| A. | x=1 | B. | x1=-1,x2=1 | C. | x1=0,x2=1 | D. | x=-1 |
8.若⊙O的半径为5,圆心O的坐标为(3,4).点P的坐标为(5,2),则P与点⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 不能确定 |
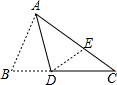 将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.
将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.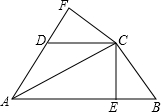 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.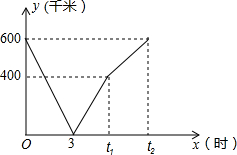 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时. 如图,若∠DAB=∠CAE,∠B=∠D,AD=4,DE=5,AB=6,求BC的长.
如图,若∠DAB=∠CAE,∠B=∠D,AD=4,DE=5,AB=6,求BC的长.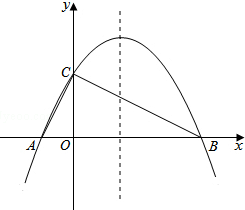 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).