题目内容
16. 某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).(1)求y关于x的函数表达式和自变量的取值范围;
(2)若长方形猪栏砖墙部分的长度为5m,求自变量x的取值范围.
分析 (1)由题意可得y关于x的函数表达式,由x>0,40-2x>0,从而可以得出x的取值范围.
(2)由题意可知,y≤5,然后根据第一问中的表达式可以确定x的取值范围.
解答 解:(1)根据题意可得,2x+y=40,
∴y=40-2x.
∴自变量x满足的条件为$\left\{\begin{array}{l}{x>0}\\{40-2x>0}\end{array}\right.$.
解不等式组得,0<x<20.
∴y关于x的函数表达式为:y=40-2x(0<x<20).
(2)由题意可得,40-2x≤5,
解得,x≥17.5.
故长方形猪栏砖墙部分的长度为5m,自变量x的取值范围为:17.5≤x<20.
点评 本题考查根据实际问题列出函数的关系式并且确定自变量的取值范围,关键是明确题意,找出相应的关系,确定自变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.对于每个非零自然数n,抛物线y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2015B2015的值是( )
| A. | 1 | B. | $\frac{1}{2015}$ | C. | $\frac{2014}{2015}$ | D. | $\frac{2015}{2016}$ |
8.若⊙O的半径为5,圆心O的坐标为(3,4).点P的坐标为(5,2),则P与点⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 不能确定 |
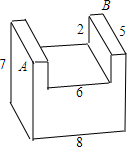 在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是13分米.
在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是13分米.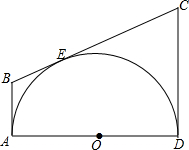 如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少?
如图所示,AD为半圆O的直径,AB,CD与半圆O相切于A,D两点,BC与半圆O相切于点E.若AB=4,CD=9,则半圆O的直径是多少?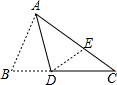 将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.
将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.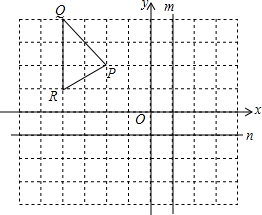 如图,每个正方形的边长都是1,分别作出△PQR关于直线x=1(记为m)和直线y=-1(记为n)对称的图形,它们的对应点的坐标之间分别有什么关系?
如图,每个正方形的边长都是1,分别作出△PQR关于直线x=1(记为m)和直线y=-1(记为n)对称的图形,它们的对应点的坐标之间分别有什么关系? 在半径为1的圆内,画一个正六边形ABCDEF,把圆平均分成六个小扇形,求每个小扇形的圆心角及扇形的面积.
在半径为1的圆内,画一个正六边形ABCDEF,把圆平均分成六个小扇形,求每个小扇形的圆心角及扇形的面积.