题目内容
一座拱桥,桥下水面宽度AB是20米,拱高CD是4米,若水面上升3米至EF处,则水面宽度EF是多少米?
(1)若把拱桥看作是抛物线的一部分,建立如图1坐标,求EF?
(2)若把拱桥看做是圆的一部分,则可构造图形,如图2所示,求EF?
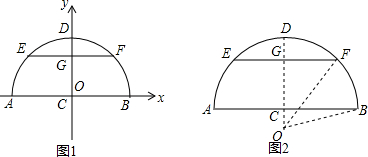
(1)若把拱桥看作是抛物线的一部分,建立如图1坐标,求EF?
(2)若把拱桥看做是圆的一部分,则可构造图形,如图2所示,求EF?
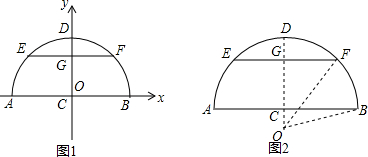
考点:垂径定理的应用,勾股定理
专题:
分析:(1)设抛物线的解析式为y=ax2+c(a≠0),再根据垂径定理求出A,D的坐标,代入抛物线的解析式求出a、c的值,再把y=3代入即可得出x的值,进而得出EF的长;
(2)设圆的半径是r米,在Rt△OCB中,易知r2=(r-4)2+102,求出r的值,在Rt△OGF中根据勾股定理求出GF的长,进而可得出EF的长.
(2)设圆的半径是r米,在Rt△OCB中,易知r2=(r-4)2+102,求出r的值,在Rt△OGF中根据勾股定理求出GF的长,进而可得出EF的长.
解答:解:(1)设抛物线的解析式为y=ax2+c(a≠0),
∵AB是20米,
∴AC=10米,拱高CD是4米,
∴A,D的坐标分别是(-10,0),(0,4)
把这两点的坐标代入解析式得,
解得a=-
,c=4,
则解析式是y=-
x2+4.
把y=3代入解析式解得x=±5,
∴EF=10米;
(2)设圆的半径是r米,在Rt△OCB中,
∵OB2=BC2+OC2,即r2=(r-4)2+102,解得r=14.5,
∴OF=14.5,OG=14.5-1=13.5,
∴GF2=OF2-OG2,即GF2=14.52-13.52=28,
∴GF=2
,此时水面宽度EF=4
米.
∵AB是20米,
∴AC=10米,拱高CD是4米,
∴A,D的坐标分别是(-10,0),(0,4)
把这两点的坐标代入解析式得,
|
解得a=-
| 1 |
| 25 |
则解析式是y=-
| 1 |
| 25 |
把y=3代入解析式解得x=±5,
∴EF=10米;
(2)设圆的半径是r米,在Rt△OCB中,
∵OB2=BC2+OC2,即r2=(r-4)2+102,解得r=14.5,
∴OF=14.5,OG=14.5-1=13.5,
∴GF2=OF2-OG2,即GF2=14.52-13.52=28,
∴GF=2
| 7 |
| 7 |
点评:本题考查的是垂径定理的应用,这类题中一般使用列方程的方法,这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
一元二次方程x2+kx-3=0的一个根是x1=1,则另一个根是( )
| A、2 | B、-2 | C、3 | D、-3 |
下列说法正确的是( )
| A、三角形两边之差大于第三边 |
| B、所有的等边三角形都是全等的 |
| C、有两个角互余的三角形是直角三角形 |
| D、正n边形的内角和为180°n-2 |
 如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.
如图所示,AC垂直BC于C,AD垂直BD于D,AD=BC,CE垂直AB,DF垂直AB,垂足分别是E,F.求证:△BCE≌△ADF.