题目内容
18．
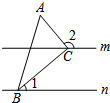如图，直线m∥n，△ABC的顶点B，C分别在直线n，m上，且AC⊥BC，若∠1=40°，则∠2的度数为（ ）
| A． | 140° | B． | 130° | C． | 120° | D． | 110° |
分析 先根据平行线的性质求出∠3的度数，再由∠ACB=90°得出∠4的度数，根据补角的定义即可得出结论．
解答 
解：∵m∥n，∠1=40°，
∴∠3=∠1=40°．
∵∠ACB=90°，
∴∠4=∠ACB-∠3=90°-40°=50°，
∴∠2=180°-∠4=180°-50°=130°．
故选B．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．
练习册系列答案
相关题目
8．已知一元二次方程x2+bx-6=0有一个根为2，则另一根为（ ）
| A． | 2 | B． | -3 | C． | 4 | D． | 3 |
9．
由6个小正方体组成了一个几何体（如图所示），如果将标有①的小正方体拿走，那么下列说法正确的是（ ）
由6个小正方体组成了一个几何体（如图所示），如果将标有①的小正方体拿走，那么下列说法正确的是（ ）| A． | 左视图不变，俯视图变化 | B． | 主视图变化，左视图不变 | ||
| C． | 左视图变化，俯视图变化 | D． | 主视图变化，俯视图不变 |
10．实数-$\sqrt{2}$的相反数是（ ）
| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | -$\frac{1}{\sqrt{2}}$ | D． | $\frac{1}{\sqrt{2}}$ |
8．
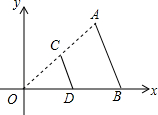如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）
如图，线段AB两个端点的坐标分别为A（6，6），B（8，0），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点C的坐标为（ ）| A． | （3，0） | B． | （4，0） | C． | （3，3） | D． | （4，3） |