题目内容
3.抛物线y=ax2+bx+c的图象向左平移5个单位或向右平移1个单位后都会经过原点,则此抛物线的对称轴与x轴的交点的横坐标是( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
分析 先根据解析式“上加下减,左加右减”的平移规律分别得到二次函数y=ax2+bx+c的图象向左平移4个单位或向右平移1个单位后的解析式,再将原点(0,0)分别代入,得25a+5b+c=0①,a-b+c=0②,再将①-②,得出b=-4a,求出-$\frac{b}{2a}$=-$\frac{-4a}{2a}$=2,进而得到二次函数y=ax2+bx+c图象的对称轴与x轴的交点坐标.
解答 解:∵y=ax2+bx+c=a(x+$\frac{b}{2a}$)2+$\frac{4ac{-b}^{2}}{4a}$,
∴二次函数y=ax2+bx+c的图象向左平移5个单位得到y=a(x+$\frac{b}{2a}$+5)2+$\frac{4ac{-b}^{2}}{4a}$,
将原点(0,0)代入,得a($\frac{b}{2a}$+5)2+$\frac{4ac{+b}^{2}}{4a}$=0,
整理,得25a+5b+c=0①.
二次函数y=ax2+bx+c的图象向右平移1个单位得到y=a(x+$\frac{b}{2a}$-1)2+$\frac{4ac{-b}^{2}}{4a}$,
将原点(0,0)代入,得a($\frac{b}{2a}$-1)2+$\frac{4ac{-b}^{2}}{4a}$=0,
整理,得a-b+c=0②.
①-②,得24a+6b=0,b=-4a,
∴-$\frac{b}{2a}$=-$\frac{-4a}{2a}$=2,
∴二次函数y=ax2+bx+c图象的对称轴与x轴的交点是(2,0).
故选A.
点评 本题考查了二次函数图象与几何变换,二次函数图象上点的坐标特征,二次函数的性质,难度适中.正确求出平移后的解析式是解题的关键.

练习册系列答案
相关题目
14.(-2)×3的结果( )
| A. | -6 | B. | 6 | C. | 5 | D. | -5 |
11.不等式组$\left\{\begin{array}{l}{x+1>2}\\{1-x≥-2}\end{array}\right.$的解集是( )
| A. | x<1 | B. | x≥3 | C. | 1≤x<3 | D. | 1<x≤3 |
18.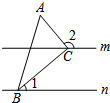 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
∠2的度数为( )
 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则∠2的度数为( )
| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
15.下面关于四边形的说法中,错误的是( )
| A. | 菱形的四条边都相等 | |
| B. | 一组邻边垂直的平行四边形是矩形 | |
| C. | 对角线相等且互相垂直的四边形是正方形 | |
| D. | 矩形是特殊的平行四边形,正方形既是特殊的矩形也是特殊的菱形 |
13.估计$\sqrt{11}$+1的值( )
| A. | 在2到3之间 | B. | 在3到4之间 | C. | 在4到5之间 | D. | 在5到6之间 |
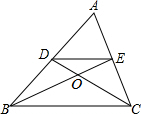 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3.
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3.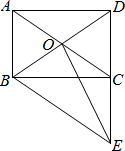 如图,矩形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,交DC的延长线于点E.
如图,矩形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,交DC的延长线于点E. 如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).
如图,直线y1=2x-1与反比例函数y2=$\frac{k}{x}$的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(-1,m).