题目内容
8.已知一元二次方程x2+bx-6=0有一个根为2,则另一根为( )| A. | 2 | B. | -3 | C. | 4 | D. | 3 |
分析 设方程的另一根为t,根据根与系数的关系得到2t=-6,然后解一次方程即可.
解答 解:设方程的另一根为t,
根据题意得2t=-6,解得t=-3.
即另一根为-3.
故选B.
点评 本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
18. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
3.用四舍五入法得到的近似数2.18×104,下列说法正确的是( )
| A. | 它精确到百分位 | B. | 它精确到百位 | C. | 它精确到万位 | D. | 它精确到0.01 |
20.已知函数y=(k-1)x2-4x+4与x轴只有一个交点,则k的取值范围是( )
| A. | k≤2且k≠1 | B. | k<2且k≠1 | C. | k=2 | D. | k=2或1 |
17.|-2016|等于( )
| A. | -2016 | B. | 2016 | C. | ±2016 | D. | -$\frac{1}{2016}$ |
18.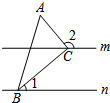 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
∠2的度数为( )
 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则∠2的度数为( )
| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
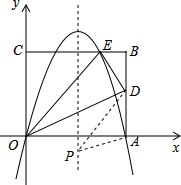 如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.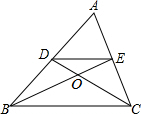 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3.
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=1:3.