题目内容
10.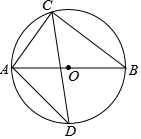 如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )
如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )| A. | 5$\sqrt{2}$ | B. | 7 | C. | 8$\sqrt{2}$ | D. | 9 |
分析 先根据圆周角定理得出∠ACB=90°,由勾股定理求出AB的长,连接BD,易得△ABD是等腰直角三角形,然后由特殊角的三角函数值,求得AD的长.
解答 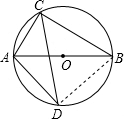 解:∵⊙O的直径为AB,
解:∵⊙O的直径为AB,
∴∠ACB=90°.
∵AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
连接BD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵CD是∠ACB的平分线,
∴∠ACD=$\frac{1}{2}$∠ACB=45°,
∴∠ABD=∠ACD=45°,
∴AD=BD,
∵AB=10,
∴AD=AB•sin45°=5$\sqrt{2}$.
故选A.
点评 此题考查了圆周角定理、等腰直角三角形的性质及勾股定理,此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
20.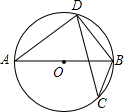 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
 如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.
如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长. 如图,点G是△ABC的重心,联结AG并延长交BC于点D,GE∥AB交BC与E,若AB=6,那么GE=2.
如图,点G是△ABC的重心,联结AG并延长交BC于点D,GE∥AB交BC与E,若AB=6,那么GE=2.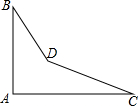 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?