题目内容
2．
如图，点G是△ABC的重心，联结AG并延长交BC于点D，GE∥AB交BC与E，若AB=6，那么GE=2．
分析 先根据点G是△ABC的重心，得出DG：DA=1：3，再根据平行线分线段成比例定理，得出$\frac{EG}{BA}$=$\frac{DG}{DA}$，即$\frac{EG}{6}$=$\frac{1}{3}$，进而得出GE的长．
解答 解：∵点G是△ABC的重心，
∴DG：AG=1：2，
∴DG：DA=1：3，
∵GE∥AB，
∴$\frac{EG}{BA}$=$\frac{DG}{DA}$，即$\frac{EG}{6}$=$\frac{1}{3}$，
∴EG=2，
故答案为：2．
点评 本题主要考查了三角形的重心以及平行线分线段成比例定理的综合应用，解题时注意：重心到顶点的距离与重心到对边中点的距离之比为2：1．
练习册系列答案
相关题目
10．
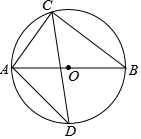如图，⊙O的直径为AB，弦AC长为6，BC长为8，∠ACB的平分线交⊙O于D，则弦AD的长为（ ）
如图，⊙O的直径为AB，弦AC长为6，BC长为8，∠ACB的平分线交⊙O于D，则弦AD的长为（ ）| A． | 5$\sqrt{2}$ | B． | 7 | C． | 8$\sqrt{2}$ | D． | 9 |
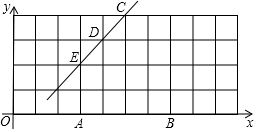足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好，己知在正方形网格中（每个正方形单位长度都为1），点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，如图建立直角坐标系，则：