题目内容
20.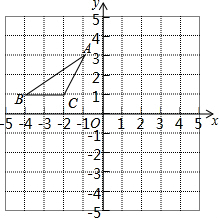 在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(-1,3)、B(-4,1)、C(-2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.
在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(-1,3)、B(-4,1)、C(-2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.(1)分别作出△A1B1C1和△A2B2C2;
(2)求△A2B2C2的面积.
分析 (1)直接利用平移的性质分别得出对应点位置进而得出答案;
(2)直接利用三角形面积求法得出答案.
解答  解:(1)如图所示:△A1B1C1和△A2B2C2,即为所求;
解:(1)如图所示:△A1B1C1和△A2B2C2,即为所求;
(2)△A2B2C2的面积为:$\frac{1}{2}$×2×2=2.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
10. 如图,已知∠1=∠B,则下列结论错误的是( )
如图,已知∠1=∠B,则下列结论错误的是( )
 如图,已知∠1=∠B,则下列结论错误的是( )
如图,已知∠1=∠B,则下列结论错误的是( )| A. | AD∥BC | B. | ∠2+∠B=180° | C. | ∠2=∠C | D. | ∠C+∠D=180° |
12.已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系,现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
(1)求y关于x的函数关系式(不需要写出函数自变量x的取值范围);
(2)用该体温计测体温时,水银柱的长度为6.0cm,求此时体温计的读数.

| 水银柱的长度x(cm) | 4.0 | … | 8.0 | 9.6 |
| 体温计的度数y(℃) | 35.0 | … | 40.0 | 42.0 |
(2)用该体温计测体温时,水银柱的长度为6.0cm,求此时体温计的读数.
9.若不等式组$\left\{\begin{array}{l}{2x-1>3}\\{x≤a}\end{array}\right.$的整数解共有三个,则a的取值范围是( )
| A. | 5≤a<6 | B. | 5<a≤6 | C. | 5<a<6 | D. | 5≤a≤6 |
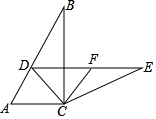 如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.
如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.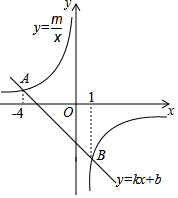 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A、B两点,其横坐标-4、1,则关于x的不等式$\frac{m}{x}$>kx+b的解集为-4<x<0或x>1.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A、B两点,其横坐标-4、1,则关于x的不等式$\frac{m}{x}$>kx+b的解集为-4<x<0或x>1. 为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )
为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )