题目内容
12.将进价为4元的小商品按5元售出时,能卖出500件,已知这种商品每件涨价1元,其销售量就减少10件,为了赚得3440元的利润,售价应定为多少?这时应进货多少件?分析 总利润=销售量×每个利润.设涨价x元能赚得3440元的利润,即售价定为每个(x+5)元,应进货(500-10x)个,根据为了赚得3440元的利润,可列方程求解.
解答 解:设涨价x元能赚得3440元的利润,即售价定为每个(x+5)元,应进货(500-10x)个,
依题意得:
(5-4+x)(500-10x)=3440,
解得x1=12,x2=47(不合题意,舍去),
当x=12时,x+5=17,500-10x=380;
答:售价定为每个17元时,应进货380件.
点评 本题考查一元二次方程的应用,关键看到涨价和销售量的关系,然后以利润做为等量关系列方程求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
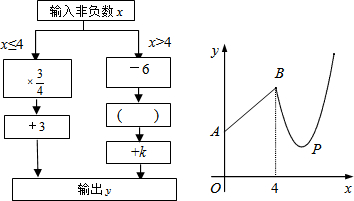
4.如图是数值转换机的示意图,小明按照其对应系画出了y与x的函数图象.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.

9.下列计算错误的是( )
| A. | (23)2×24=210 | B. | (-c)3(-c)5=c8 | C. | 32×(-3)4=(-3)6 | D. | 5×(-$\frac{1}{2}$)2=20 |

 如图,P为正方形ABCD边CD上一点,∠BAP的平分线交BC于点Q,说明:AP=DP+BQ.
如图,P为正方形ABCD边CD上一点,∠BAP的平分线交BC于点Q,说明:AP=DP+BQ. 如图所示,山坡AB的坡度为5:12,一辆汽车从山脚A处出发,把货物运到高度为75m的山顶B处,求汽车从A到B所行驶的路程.
如图所示,山坡AB的坡度为5:12,一辆汽车从山脚A处出发,把货物运到高度为75m的山顶B处,求汽车从A到B所行驶的路程.