题目内容
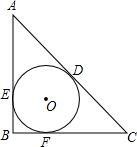 ⊙O是△ABC的内切圆,D、E、F为切点,AB=12cm,BC=14cm,CA=18cm.求AE、BF、CD的长.
⊙O是△ABC的内切圆,D、E、F为切点,AB=12cm,BC=14cm,CA=18cm.求AE、BF、CD的长.考点:三角形的内切圆与内心
专题:
分析:利用切线长定理得出设AE=AD=x,则BF=BE=(12-x)cm,FC=DC=(18-x)cm,进而得出即可.
解答:解:∵⊙O是△ABC的内切圆,D、E、F为切点,AB=12cm,BC=14cm,CA=18cm,
∴AE=AD,BE=BF,CF=CD,
设AE=AD=x,则BF=BE=(12-x)cm,FC=DC=(18-x)cm,
则BC=BF+FC=12-x+18-x=14,
解得:x=8,
故BE=BF=12-8=4(cm),CD=FC=18-8=10(cm),
故AE=8cm,BF=4cm,DC=10cm.
∴AE=AD,BE=BF,CF=CD,
设AE=AD=x,则BF=BE=(12-x)cm,FC=DC=(18-x)cm,
则BC=BF+FC=12-x+18-x=14,
解得:x=8,
故BE=BF=12-8=4(cm),CD=FC=18-8=10(cm),
故AE=8cm,BF=4cm,DC=10cm.
点评:此题主要考查了切线长定理,用一个未知数表示出各边长是解题关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
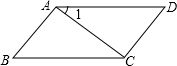 如图,∠1=25°,∠B=65°,AB⊥AC.
如图,∠1=25°,∠B=65°,AB⊥AC.