题目内容
4. 如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
分析 小球滚动的速度与机器人行走的速度相等,运动时间相等,得出BC=AC,由勾股定理可求得BC的长.
解答 解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,即BC=CA,设AC为x,则OC=(45-x),
由勾股定理可知OB2+OC2=BC2,
又∵OA=45,OB=15,
把它代入关系式152+(45-x)2=x2,
解方程得出x=25(cm).
答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25cm.
点评 本题考查了勾股定理的应用,理解题意找出等量关系是解题关键,再由勾股定理即可得到答案.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19. 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
9.下列关于$\sqrt{8}$的说法中,不正确的是( )
| A. | $\sqrt{8}$是无理数 | B. | $\sqrt{8}$的大小介于2和3之间 | ||
| C. | $\sqrt{8}$可以用数轴上的点表示 | D. | $\sqrt{8}$是$\sqrt{2}$的4倍 |
16.为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球的单价为1.5元,乒乓球拍的单价为25元,如果购买总金额不超过200元,且尽可能多的购买乒乓球拍,则小张同学最多可购买乒乓球拍( )
| A. | 5副 | B. | 6副 | C. | 7副 | D. | 8副 |
13.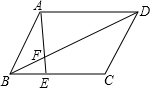 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
 如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )
如图,点E是平行四边形ABCD边BC上一点,BE:EC=4:1,AE交BD于F点,BF:FD等于( )| A. | 4:5 | B. | 4:9 | C. | 5:9 | D. | 4:10 |
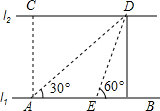 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.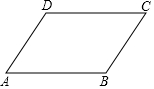 已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.
已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.