题目内容
6.计算:$\frac{1}{x}$÷($\frac{{x}^{2}+1}{{x}^{2}-x}$-$\frac{2}{x-1}$)+$\frac{1}{x-1}$,其中x=$\sqrt{2}$.分析 首先进行通分运算,进而因式分解法再化简分式,最后把已知x的值代入求出答案.
解答 解:$\frac{1}{x}$÷($\frac{{x}^{2}+1}{{x}^{2}-x}$-$\frac{2}{x-1}$)+$\frac{1}{x-1}$,
=$\frac{1}{x}$÷[$\frac{{x}^{2}+1}{x(x-1)}$-$\frac{2x}{x(x-1)}$]+$\frac{1}{x-1}$
=$\frac{1}{x}$÷$\frac{(x-1)^{2}}{x(x-1)}$+$\frac{1}{x-1}$
=$\frac{1}{x-1}$+$\frac{1}{x-1}$
=$\frac{2}{x-1}$,
把x=$\sqrt{2}$代入得:
原式=$\frac{2}{\sqrt{2}-1}$=2$\sqrt{2}$+2.
点评 此题主要考查了分式的化简求值,正确分解因式再化简分式是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16. 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
 如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )
如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )| A. | 中位数是6.5 | |
| B. | 平均数高于众数 | |
| C. | 极差为3 | |
| D. | 平均每周锻炼超过6小时的人占总数的一半 |
14.2014年吉林省对全省供热管网进行改造,改造后全年二氧化碳排放量共减少7620000吨,7620000这个数用科学记数法表示为( )
| A. | 762×104 | B. | 76.2×105 | C. | 7.62×106 | D. | 0.762×107 |
11. 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
 如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )
如图,直线a∥b,∠1=80°,∠2=40°,则∠3等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
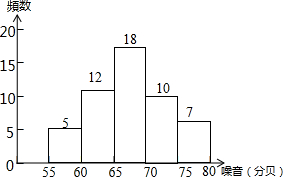 未调查居民生活环境状况,环保局对所辖的52个居民区进行了噪音(单位:分贝)水平的调查,结果如图.
未调查居民生活环境状况,环保局对所辖的52个居民区进行了噪音(单位:分贝)水平的调查,结果如图.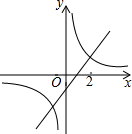 如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).
如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).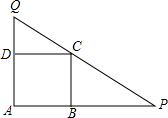 如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.