题目内容
9.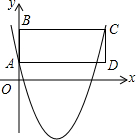 如图,在平面直角坐标系中,抛物线y=ax2-4ax+1(a>0)与y轴交于点A,点D的坐标为($\frac{2}{a}$,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD.
如图,在平面直角坐标系中,抛物线y=ax2-4ax+1(a>0)与y轴交于点A,点D的坐标为($\frac{2}{a}$,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD.(1)当点B的坐标为(0,2)时,求抛物线对应的函数表达式.
(2)当矩形ABCD的边AD被抛物线分成1:3两部分时,求点C的坐标.
(3)当矩形ABCD是正方形时,求a的值.
(4)在抛物线的对称轴上有一点P,当△ABP为等腰直角三角形时,求点P的坐标.
分析 (1)由题意易得点C的坐标为:($\frac{2}{a}$,2),然后代入抛物线y=ax2-4ax+1,即可求得答案;
(2)首先设抛物线交AD于点E,则点E的纵坐标为1,可求得点E的坐标,然后分别从AE=3DE或3AE=DE去分析求解即可求得答案;
(3)若矩形ABCD是正方形,则AD=CD,可求得点C的坐标,然后分别从点C在点D上方与点C在点D下方,去分析求解即可求得答案;
(4)分别从∠BAP=90°,∠ABP=90°或∠APB=90°,去分析求解即可求得答案.
解答 解:(1)∵CB∥x轴,DC∥y轴,点B的坐标为(0,2),点D的坐标为($\frac{2}{a}$,1),
∴点C的坐标为:($\frac{2}{a}$,2),
∵抛物线y=ax2-4ax+1(a>0)过点C,
∴$\frac{4}{a}$-8+1=2,
解得:a=$\frac{4}{9}$,
∴抛物线对应的函数表达式为:y=$\frac{4}{9}$x2-$\frac{16}{9}$x+1;
(2)设抛物线交AD于点E,则点E的纵坐标为1,
由ax2-4ax+1=1,
解得:x1=0,x2=4,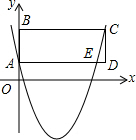
∴点E的坐标为(4,1),
∵点D的坐标为($\frac{2}{a}$,1),
则DE=$\frac{2}{a}$-4,
当AE=3DE时,4=3($\frac{2}{a}$-4),
解得:a=$\frac{3}{8}$,
∴点C的坐标为:($\frac{16}{3}$,$\frac{11}{3}$);
当3AE=DE时,12=$\frac{2}{a}$-4,
解得:a=$\frac{1}{8}$,
∴点C的坐标为:(16,25);
(3)若矩形ABCD是正方形,则AD=CD,
∵点D的坐标为:($\frac{2}{a}$,1),且DC∥y轴,
∴C($\frac{2}{a}$,$\frac{4}{a}$-7),
若点C在点D上方,则CD=$\frac{4}{a}$-8,
∴$\frac{2}{a}$=$\frac{4}{a}$-8,
解得:a=$\frac{1}{4}$;
若点C在点D下方,则CD=8-$\frac{4}{a}$,
∴$\frac{2}{a}$=8-$\frac{4}{a}$,
解得:a=$\frac{3}{4}$;
综上可得:a=$\frac{1}{4}$或$\frac{3}{4}$;
(4)抛物线的对称轴方程为:x=-$\frac{b}{2a}$=-$\frac{-4a}{2a}$=2,
∵△ABP为等腰直角三角形,
∴若∠BAP=90°,则点P的坐标为:(2,1);
若∠ABP=90°,则AB=BP=2,
∴点P的坐标为:(2,3)或(2,-1);
若∠APB=90°,AB=2×2=4,
∴点P的坐标为:(2,3);
综上所述:点P的坐标为:(2,1)或(2,3)或(2,-1).
点评 此题属于二次函数的综合题.考查了待定系数求二次函数解析式、矩形的性质、正方形的性质以及等腰直角三角形性质.注意掌握分类讨论思想的应用是解此题的关键.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案①正三角形都相似;②含45°的直角三角形都相似; ③含30°的直角三角形都相似; ④直角三角形斜边上的高分原三角形成的两个小三角形相似;⑤菱形都相似;⑥矩形都相似;⑦正方形都相似;⑧圆形都相似.
| A. | ①②③④⑦⑧ | B. | ①②③⑦⑧ | C. | ②③⑥⑦⑧ | D. | ①④⑤⑦⑧ |
| A. |  | B. |  | C. |  | D. |  |
| A. | 762×104 | B. | 76.2×105 | C. | 7.62×106 | D. | 0.762×107 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第一、三象限 |
 请把下面的小船图案先向上平移3格,再向右平移4格,最后为这个图案配上一句简短的解说词.
请把下面的小船图案先向上平移3格,再向右平移4格,最后为这个图案配上一句简短的解说词.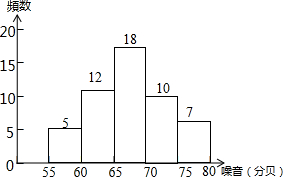 未调查居民生活环境状况,环保局对所辖的52个居民区进行了噪音(单位:分贝)水平的调查,结果如图.
未调查居民生活环境状况,环保局对所辖的52个居民区进行了噪音(单位:分贝)水平的调查,结果如图.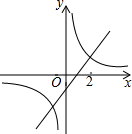 如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).
如图,反比例函数y1=$\frac{{k}_{1}}{x}$的图象与直线y2=k2x+b的一个交点的横坐标为2,当x=3时,y1<y2(填“>”、“=”或“<”).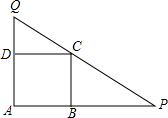 如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.