题目内容
18.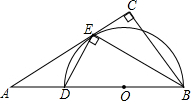 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=2$\sqrt{3}$,AE=6,求EC的长.
分析 (1)取BD的中点0,连结OE,如图,由∠BED=90°,根据圆周角定理可得BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,再证明OE∥BC,得到∠AEO=∠C=90°,于是可根据切线的判定定理判断AC是△BDE的外接圆的切线;
(2)设⊙O的半径为r,根据勾股定理得62+r2=(r+2$\sqrt{3}$)2,解得r=2$\sqrt{3}$,根据平行线分线段成比例定理,由OE∥BC得$\frac{AE}{CE}$=$\frac{AO}{OB}$,然后根据比例性质可计算出EC.
解答 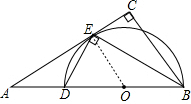 (1)证明:取BD的中点0,连结OE,如图,
(1)证明:取BD的中点0,连结OE,如图,
∵DE⊥EB,
∴∠BED=90°,
∴BD为△BDE的外接圆的直径,点O为△BDE的外接圆的圆心,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠EB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴OE⊥AE,
∴AC是△BDE的外接圆的切线;
(2)解:设⊙O的半径为r,则OA=OD+DA=r+2$\sqrt{3}$,OE=r,
在Rt△AEO中,∵AE2+OE2=AO2,
∴62+r2=(r+2$\sqrt{3}$)2,解得r=2$\sqrt{3}$,
∵OE∥BC,
∴$\frac{AE}{CE}$=$\frac{AO}{OB}$,即$\frac{6}{CE}$=$\frac{4\sqrt{3}}{2\sqrt{3}}$,
∴CE=3.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和平行线分线段成比例定理.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
6.若x>y,则下列式子中错误的是( )
| A. | x-3>y-3 | B. | x+3>y+3 | C. | -3x>-3y | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
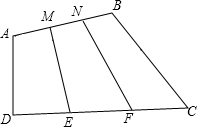 如图,四边形ABCD的面积为1,E,F,M,N分别为CD,AB的三等分点,求四边形EFNM的面积.
如图,四边形ABCD的面积为1,E,F,M,N分别为CD,AB的三等分点,求四边形EFNM的面积. 已知在△ABC中,AB=4,AC=3,AB与AC的夹角为α,设△ABC的面积为S.
已知在△ABC中,AB=4,AC=3,AB与AC的夹角为α,设△ABC的面积为S.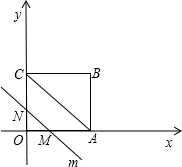 如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).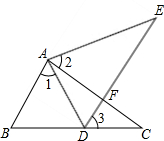 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,请找出图中的全等三角形,并给予证明.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,请找出图中的全等三角形,并给予证明.