题目内容
8．
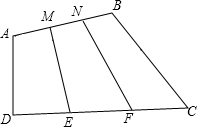如图，四边形ABCD的面积为1，E，F，M，N分别为CD，AB的三等分点，求四边形EFNM的面积．
分析 连接DB，DE，EN，NB，利用等高的两个三角形面积比等于底边之比，求出四边形DEBN的面积与四边形ABCD的面积关系，利用三角形的中线性质求出四边形EFNM的面积与四边形DEBN的面积关系．
解答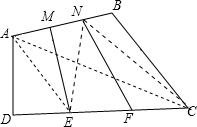 
解：连接DB，DE，EN，NB，
则S△BDE=$\frac{2}{3}$S△ABD，S△BDN=$\frac{2}{3}$S△BCD，得S四边形DEBN=$\frac{2}{3}$S四边形ABCD=$\frac{2}{3}$，
又S△EMN=S△EMD，S△EFN=S△BFN，
∴S四边形EFNM=$\frac{1}{2}$S四边形DEBN=$\frac{1}{3}$．
点评 本题考查了三角形面积的性质．关键是将求四边形的面积问题转化为求三角形的面积，利用等高的两个三角形面积比等于底边之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．若关于x的一元二次方程2x2-x-n=0没有实数根，则二次函数y=2x2-x-n的图象的顶点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
已知A（-2，0），B（4，0），C的坐标为（x，y），且S△ABC=12，|x|=3，求C点的坐标．
20．
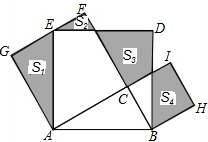如图，Rt△ABC中，∠C=90°，AC=12，BC=5．分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH，四块阴影部分的面积分别为S1、S2、S3、S4． 则S1+S2+S3+S4等于（ ）
如图，Rt△ABC中，∠C=90°，AC=12，BC=5．分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH，四块阴影部分的面积分别为S1、S2、S3、S4． 则S1+S2+S3+S4等于（ ）| A． | 90 | B． | 60 | C． | 169 | D． | 144 |
17．在下列各式的变形中，正确的是（ ）
| A． | （-x-y）（-y+x）=-x2-y2 | B． | x2-2x-3=（x-1）2-4 | C． | $1-\frac{1}{x}=x-1$ | D． | （x-y）-1=y-x |
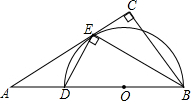如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．