��Ŀ����
8�� ���κ���y=ax2+bx+c��ͼ���㣨-1��4��������ֱ��y=-$\frac{1}{2}$x+1�ཻ��A��B���㣨��ͼ����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C��-3��0����
���κ���y=ax2+bx+c��ͼ���㣨-1��4��������ֱ��y=-$\frac{1}{2}$x+1�ཻ��A��B���㣨��ͼ����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C��-3��0������1������κ����ı���ʽ��
��2����N�Ƕ��κ���ͼ����һ�㣨��N��AB�Ϸ�������N��NP��x�ᣬ����Ϊ��P����AB�ڵ�M����MN�����ֵ��
��3���ڣ�2���������£��Ƿ���ڵ�N��ʹ��BM��NC���ֱƽ�֣������ڣ������������������N������ꣻ�������ڣ�˵�����ɣ�
���� ��1����һ�κ�����ϵʽ��x=0��x=-3�������A��B�����꣬��������������ô���ϵ�������ɵó����ۣ�
��2�����N������Ϊ��m��-$\frac{5}{4}{m}^{2}$-$\frac{17}{4}$m+1����-3��m��0�������M������Ϊ��m��-$\frac{1}{2}$m+1�����ú�m�Ĵ���ʽ��ʾ����MN����϶��κ��������ʼ��ɽ����ֵ���⣻
��3��������ڣ����N������Ϊ��m��-$\frac{5}{4}{m}^{2}$-$\frac{17}{4}$m+1����-3��m��0��������BN��CM�����ı���BCMNΪ����ʱ��BM��NC���ֱƽ�֣�����BC=MN���m��ֵ���Ӷ��ó���N�����꣬��ȥ��֤BN�Ƿ����BC���ɴ˼��ɵó����ۣ�
��� �⣺��1����һ�κ���y=-$\frac{1}{2}$x+1��x=0����y=1��
���A��������0��1����
��һ�κ���y=-$\frac{1}{2}$x+1��x=-3����y=-$\frac{1}{2}$����-3��+1=$\frac{5}{2}$��
���B��������-3��$\frac{5}{2}$����
����A��0��1������B��-3��$\frac{5}{2}$�����㣨-1��4�����뵽y=ax2+bx+c�У�
�ã�$\left\{\begin{array}{l}{1=c}\\{\frac{5}{2}=9a-3b+c}\\{4=a-b+c}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-\frac{5}{4}}\\{b=-\frac{17}{4}}\\{c=1}\end{array}\right.$��
����κ����ı���ʽΪy=-$\frac{5}{4}{x}^{2}$-$\frac{17}{4}$x+1��
��2�����N��������m��-$\frac{5}{4}{m}^{2}$-$\frac{17}{4}$m+1����-3��m��0�������M��������m��-$\frac{1}{2}$m+1����
��MN=-$\frac{5}{4}{m}^{2}$-$\frac{17}{4}$m+1-��-$\frac{1}{2}$m+1��=-$\frac{5}{4}{m}^{2}$-$\frac{15}{4}$m=-$\frac{5}{4}$$��m+\frac{3}{2}��^{2}$+$\frac{45}{16}$��
�൱m=-$\frac{3}{2}$ʱ��MNȡ���ֵ�����ֵΪ$\frac{45}{16}$��
��3��������ڣ����N������Ϊ��m��-$\frac{5}{4}{m}^{2}$-$\frac{17}{4}$m+1����-3��m��0��������BN��CM����ͼ��ʾ��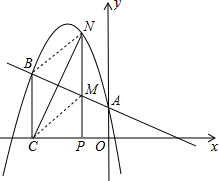
��ҪBM��NC���ֱƽ�֣�ֻ���ı���BCMNΪ���μ��ɣ�
�ߵ�B����Ϊ��-3��$\frac{5}{2}$������C������Ϊ��-3��0����
��BC=$\frac{5}{2}$��
���ı���BCMNΪ���Σ�
��MN=-$\frac{5}{4}{m}^{2}$-$\frac{15}{4}$m=BC=$\frac{5}{2}$��
��ã�m1=-2��m2=-1��
��m=-2ʱ����N������Ϊ��-2��$\frac{9}{2}$����
��BN=$\sqrt{[-2-��-3��]^{2}+��\frac{9}{2}-\frac{5}{2}��^{2}}$=$\sqrt{5}$��BC=$\frac{5}{2}$��BN��BC��
��m=-2����ȥ����
��m=-1ʱ����N������Ϊ��-1��4����
��BN=$\sqrt{[-1-��-3��]^{2}+��4-\frac{5}{2}��^{2}}$=$\frac{5}{2}$��BC=$\frac{5}{2}$��BN=BC��
���N��-1��4���������⣮
�ʴ��ڵ�N��ʹ��BM��NC���ֱƽ�֣���N������Ϊ��-1��4����
���� ���⿼���˴���ϵ������������ʽ�����κ����������Լ����ε����ʣ�����Ĺؼ��ǣ���1�������A��B�����ꣻ��2�����ö��κ��������ʽ����ֵ���⣻��3���������ε�����ȷ����N�����꣮���������е��⣬��1����2���ѶȲ���3����ȷ�������ı���BCMN����״������͵��Խ���������������Ŀʱ������Ҫ�뵽���ǽ�BM��NC���ɶԽ��ߣ����ݶԽ����ഹֱƽ�����жϳ��ı�����ʲô��״���ٸ��ݸ���״ͼ�ε���������ȥ������⣮

| A�� | 3��7��8 | B�� | 4��5��6 | C�� | 6��8��15 | D�� | 8��9��15 |
| A�� | ���������� | B�� | ���������� | ||
| C�� | ͼ����ԭ���һ�κ��� | D�� | ���κ��� |
 ��ͼ�������ϵ�A��B��C��D�ĵ��У����ʾ��-$\sqrt{5}$�ĵ���ӽ����ǣ�������
��ͼ�������ϵ�A��B��C��D�ĵ��У����ʾ��-$\sqrt{5}$�ĵ���ӽ����ǣ�������| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |