Question

7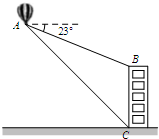．如图，在热气球上A处测得一栋大楼顶部B的俯角为23°，测得这栋大楼底部C的俯角为45°．已知热气球A处距地面的高度为180m，求这栋大楼的高度（精确到1m）．参考数据：sin23°=0.39，cos23°=0.92，tan23°=0.42．

Answer 1

分析 首先过P作PC⊥AB，垂足为C，进而求出DC的长，利用tan23°=$\frac{BD}{PC}$，得BD的长，即可得出答案．

解答 解：过点A作直线BC的垂线，垂足为点D，
由题意，得∠CAD=45°，∠BAD=23°，CD=180，
∴∠CAD=∠ACD=45°，
∴CD=AD=180，
在Rt△ABD中，∠BDA=90°$tan∠BAD=\frac{BD}{AD}=0.42$，
∴BD=0.42×180=75.6，
∴BC=CD-BD=180-75.6=104.4≈104m，
答：这栋大楼的高约为104m．

点评 此题主要考查了解直角三角形的应用，根据题意正确构造直角三角形是解题关键．