题目内容
11.二次函数y=ax2+bx+c(a>0)的顶点为P,其图象与x轴有两个交点A(-m,0),B(1,0),交y轴于点C(0,-3am+6a),以下说法:①m=3;
②当∠APB=120°时,a=$\frac{\sqrt{3}}{6}$;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥$\frac{1}{2}$
正确的是( )
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
分析 ①把A、B两点的坐标分别代入抛物线的解析式得到①式和②式,将两式相减即可得到m=$\frac{a+b}{a}$,即可得到C(0,3a-3b),从而得到c=3a-3b,代入②式,就可解决问题;
②设抛物线的对称轴与x轴的交点为G,则有PG⊥x轴,只需求出点P的坐标就可解决问题;
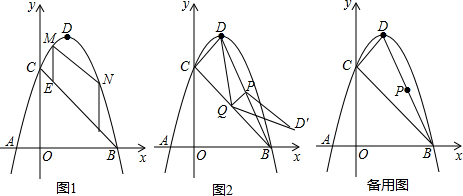
③在第一象限内作∠MBA=120°,且满足BM=BA,过点M作MH⊥x轴于H,如图1,只需求出点M的坐标,然后验证点M是否在抛物线上,就可解决问题;
④易知点N在抛物线上且△ABN为直角三角形时,只能∠ANB=90°,此时点N在以AB为直径的⊙G上,因而点N在⊙G与抛物线的交点处,要使点N存在,点P必须在⊙G上或⊙G外,如图2,只需根据点与圆的位置关系就可解决问题.
解答 解:①∵点A(-m,0)、B(1,0)在抛物线y=ax2+bx+c上,
∴$\left\{\begin{array}{l}{a{m}^{2}-bm+c=0①}\\{a+b+c=0②}\end{array}\right.$,
由①-②得
am2-bm-a-b=0,
即(m+1)(am-a-b)=0.
∵A(-m,0)与B(1,0)不重合,
∴-m≠1即m+1≠0,
∴m=$\frac{a+b}{a}$,
∴点C的坐标为(0,3a-3b),
∵点C在抛物线y=ax2+bx+c上,
∴c=3a-3b,
代入②得a+b+3a-3b=0,即b=2a,
∴m=$\frac{a+b}{a}$=3,故①正确;
②∵m=3,∵A(-3,0),
∴抛物线的解析式可设为y=a(x+3)(x-1),
则y=a(x2+2x-3)=a(x+1)2-4a,
∴顶点P的坐标为(-1,-4a).
根据对称性可得PA=PB,
∴∠PAB=∠PBA=30°.
设抛物线的对称轴与x轴的交点为G,
则有PG⊥x轴,
∴PG=AG•tan∠PAG=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴4a=$\frac{2\sqrt{3}}{3}$,
∴a=$\frac{\sqrt{3}}{6}$,故②正确;
③在第一象限内作∠MBA=120°,且满足BM=BA,过点M作MH⊥x轴于H,如图1,
在Rt△MHB中,∠MBH=60°,
则有MH=4sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,BH=4cos60°=4×$\frac{1}{2}$=2,
∴点M的坐标为(3,2$\sqrt{3}$),
当x=3时,y=$\frac{\sqrt{3}}{6}$(3+3)(3-1)=2$\sqrt{3}$,
∴点M在抛物线上,故③正确;
④∵点N在抛物线上,∴∠ABN≠90°,∠BAN≠90°.
当△ABN为直角三角形时,∠ANB=90°,
此时点N在以AB为直径的⊙G上,
因而点N在⊙G与抛物线的交点处,
要使点N存在,点P必须在⊙G上或⊙G外,如图2,
则有PG≥2,即4a≥2,也即a≥$\frac{1}{2}$,故④正确.
故选D.
点评 本题主要考查了抛物线上点的坐标特征、因式分解、三角函数、圆周角定理、点与圆的位置关系等知识,运用因式分解法求m是解决①的关键,将∠ANB=90°转化为点N在以AB为直径的圆上是解决④的关键.

| A. | y=3x | B. | y=-3x | C. | $y=\frac{3}{x}$ | D. | $y=-\frac{3}{x}$ |
 如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )| A. | 70° | B. | 60° | C. | 50° | D. | 55° |
| A. | (6n+30)人 | B. | (6n-30)人 | C. | (30-6n)人 | D. | 6n人 |
| A. | a3+a3=a6 | B. | a3•a=a4 | C. | a6÷a2=a3 | D. | (2a2)3=6a5 |
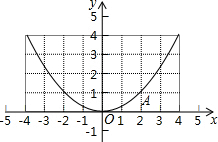 如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),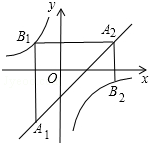 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$ 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2016=$\frac{1}{2}$.