题目内容
4.四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠BAD=90°,则△BDC为直角三角形.分析 连接BD.先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明∠DBC=90°.
解答  解:如图,分两种情况讨论,
解:如图,分两种情况讨论,
连接BD.
∵AD=3,AB=4,∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5,
∵BC=12,CD=13,
∴BD2+BC2=52+122=169,CD2=132,
∴∠DBC=90°,即△BDC为直角三角形.
故答案为直角.
点评 此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握勾股定理及勾股定理的逆定理是解本题的关键.

练习册系列答案
相关题目
19. 如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
 如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
如图,在△ABC中,D是BC上延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )| A. | 20° | B. | 30° | C. | 70° | D. | 80° |
9.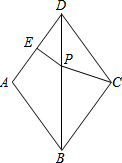 如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
 如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )| A. | 108° | B. | 72° | C. | 90° | D. | 100° |
16.绝对值为2的实数是( )
| A. | 2 | B. | 2 | C. | -2 | D. | ±2 |
14.计算(-x-2y)2-(x-2y)2的结果是( )
| A. | -8xy | B. | -2x2-8y2 | C. | 8xy | D. | 4xy |
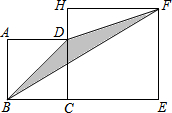 如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.
如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF. 小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.
小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.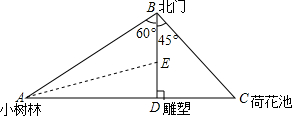 某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:
某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC: